To obtain the transport law ![]() , the mesoscopic flow
is analyzed in the limits of low and high frequencies. These limits are then connected
using a frequency function that respects causality constraints. The linear fluid
response inside the patchy composite due to a seismic wave can always be resolved
into two portions: (1) a vectorial response due to macroscopic
fluid-pressure gradients across an averaging
volume that generate a macroscopic Darcy flux
, the mesoscopic flow
is analyzed in the limits of low and high frequencies. These limits are then connected
using a frequency function that respects causality constraints. The linear fluid
response inside the patchy composite due to a seismic wave can always be resolved
into two portions: (1) a vectorial response due to macroscopic
fluid-pressure gradients across an averaging
volume that generate a macroscopic Darcy flux ![]() across each
phase and that corresponds to the macroscopic conditions
across each
phase and that corresponds to the macroscopic conditions
![]() and
and ![]() ; and (2) a scalar response
associated with internal fluid transfer and that corresponds to the macroscopic conditions
; and (2) a scalar response
associated with internal fluid transfer and that corresponds to the macroscopic conditions
![]() and
and ![]() .
The macroscopic isotropy of the composite guarantees that there is no cross-coupling
between the vectorial transport
.
The macroscopic isotropy of the composite guarantees that there is no cross-coupling
between the vectorial transport ![]() and
the scalar transport
and
the scalar transport ![]() within each sample.
within each sample.
The mesoscopic flow problem that defines ![]() is the internal equilibration of fluid
pressure between the patches when a confining pressure
is the internal equilibration of fluid
pressure between the patches when a confining pressure ![]() has
been applied to a sealed sample of the composite.
Having the external surface sealed is equivalent to the required
macroscopic constraint that
has
been applied to a sealed sample of the composite.
Having the external surface sealed is equivalent to the required
macroscopic constraint that ![]() .
Upon taking the
divergence of (2) and using equation (3), the diffusion problem
controling the mesoscopic flow becomes
.
Upon taking the
divergence of (2) and using equation (3), the diffusion problem
controling the mesoscopic flow becomes
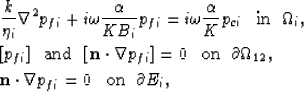 |
(56) | |
| (57) | ||
| (58) |
| (59) |