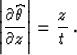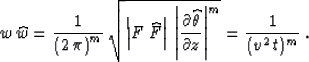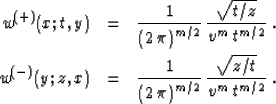Post-Stack Time Migration

An interesting example of a stacking operator is the hyperbola summation used for time migration in the post-stack domain. In this case, the summation path is defined as  

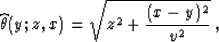$$\widehat{\theta}(y;z,x) = \sqrt{z^2+{{(x-y)^2}\over {v^2}}}\;,$$ (63)

where z denotes the vertical traveltime, x and y are the horizontal coordinates on the migrated and unmigrated sections respectively, and v stands for the effectively constant root-mean-square velocity Claerbout (1995b). The summation path for the reverse transformation (demigration) is found from solving equation (63) for z. It has the well-known elliptic form

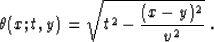$$\theta(x;t,y) = \sqrt{t^2-{{(x-y)^2}\over {v^2}}}\;.$$ (64)

The Jacobian of transforming z to t is  

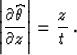$$\left\vert\partial \widehat{\theta} \over \partial z\right\vert = {z \over t}\;.$$ (65)

If the migration weighting function is defined by conventional downward continuation Schneider (1978), it takes the following form, which is equivalent to equation (44):  

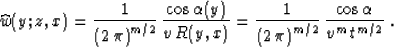$$\widehat{w}(y;z,x) = {1\over{\left(2\,\pi\right)^{m/2}}} \, ... ...2\,\pi\right)^{m/2}}} \, {\cos{\alpha} \over {v^m\,t^{m/2}}}\;.$$ (66)

The simple trigonometry of the reflected ray suggests that the cosine factor in formula (66) is equal to the simple ratio between the vertical traveltime z and the zero-offset reflected traveltime t:  

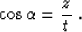$$\cos{\alpha} = {z \over t}\;.$$ (67)

The equivalence of the Jacobian (65) and the cosine factor (67) has important interpretations in the theory of Stolt frequency-domain migration Chun and Jacewitz (1981); Levin (1986); Stolt (1978). According to equation (19), the weighting function of the adjoint operator is the ratio of (66) and (65):  

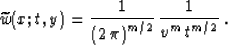$$\widetilde{w}(x;t,y) = {1\over{\left(2\,\pi\right)^{m/2}}} \, {1 \over {v^m\,t^{m/2}}}\;.$$ (68)

We can see that the cosine factor z/t disappears from the adjoint weighting. This is completely analogous to the known effect of ``dropping the Jacobian'' in Stolt migration Harlan (1983); Levin (1994). The product of the weighting functions for the time migration and its asymptotic inverse is defined according to formula (9) as  

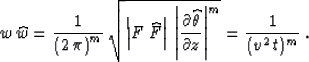$$w\,\widehat{w}={1\over{\left(2\,\pi\right)^m}} \, {\sqrt{\l... ...ta} \over \partial z\right\vert^m}} = {1 \over {(v^2\,t)^m}}\;.$$ (69)

Thus, the asymptotic inverse of the conventional time migration has the weighting function determined from equations (9) and (66) as  

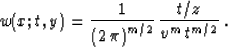$$w(x;t,y) = {1\over{\left(2\,\pi\right)^{m/2}}} \, {{t/z} \over {v^m\,t^{m/2}}}\;.$$ (70)

The weighting functions of the asymptotic pseudo-unitary operators are obtained from formulas (34) and (35). They have the form

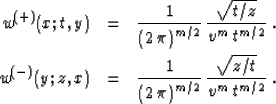$$\begin{eqnarray} w^{(+)}(x;t,y) & = & {1\over{\left(2\,\pi\right)^{m/2}}} \, {\... ...eft(2\,\pi\right)^{m/2}}} \, {\sqrt{z/t} \over {v^m\,t^{m/2}}}\;.\end{eqnarray}$$ (71) (72)

The square roots of the cosine factor appearing in formulas (71) and (72) correspond to the analogous terms in the pseudo-unitary Stolt migration proposed by Harlan and Sword 1986.