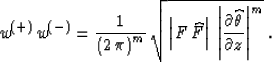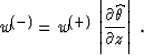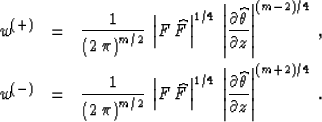Next: EXAMPLES
Up: Fomel: Stacking operators
Previous: PULL ADJOINTS
According to the theory of asymptotic inversion, briefly reviewed in
the first part of this paper, the weighting function of the
asymptotically inverse operator is inversely proportional to the
weighting of the forward operator. On the other hand, the weighting in
the ``pull'' adjoint is directly proportional to the forward
weighting. This difference allows us to define a hybrid type of
operator, which possesses both the property of being adjoint and the
property of being asymptotic inverse. It is appropriate to call a pair
of operators defined in this way asymptotic pseudo-unitary. The
definition of asymptotic pseudo-unitary operators follows directly
from the combination of definitions (7) and
(20). Splitting the derivative operator 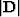 in
(7) into the product of two operators, we can write the
forward operator as
in
(7) into the product of two operators, we can write the
forward operator as
| ![\begin{displaymath}
S(t,y)= {\bf A}\left[M(z,x)\right]=
\int\,w^{(+)}(x;t,y)\,\vert{\bf D}\vert^{m/2}\,M(\theta(x;t,y),x)\,dx\end{displaymath}](img37.gif) |
(30) |
and its asymptotic pseudo-unitary adjoint as
| ![\begin{displaymath}
\widetilde{M}(z,x)={\bf \widetilde{A}}[S(t,y)]=
\vert{\bf D}...
...m/2}\;\int\,w^{(-)}(y;z,x)\,S(\widehat{\theta}(y;z,x),y)\;dy\;.\end{displaymath}](img38.gif) |
(31) |
According to equation (9),
| 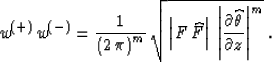 |
(32) |
According to equation (19),
| 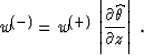 |
(33) |
Combining equations (32) and (33) uniquely determines
both weighting functions, as follows:
| 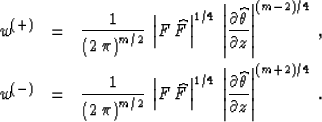 |
(34) |
| (35) |
Equations (34) and (35) complete the definition of asymptotic
pseudo-unitary operators.
The notion of pseudo-unitary operators is directly applicable in the
situations where we can arbitrarily construct both forward and inverse
operators. One example of such a situation is the velocity transform
considered in the next section of this paper. In the more common
case, the forward operator is strictly defined by the physics of a
problem. In this case, we can include asymptotic inversion in the
iterative least-square inversion by means of
preconditioning. The linear preconditioning operator should transform
the forward stacking-type operator to the form (30) with the
weighting function (34). Theoretically, this form of preconditioning leads to the fastest
convergence of the iterative least-square inversion with respect to
the high-frequency parts of the model.





Next: EXAMPLES
Up: Fomel: Stacking operators
Previous: PULL ADJOINTS
Stanford Exploration Project
9/11/2000