




Next: PULL ADJOINTS
Up: Fomel: Stacking operators
Previous: THEORETICAL DEFINITION OF A
Mathematical analysis of the inverse problem for operator
(1) shows that only in rare cases can we obtain a
theoretically exact inversion. A well-known example is the Radon
transform, which has acquired a lot of different aliases in
geophysical literature: slant stack, tau-p transform, plane wave
decomposition, and controlled directional reception (CDR) transform
Gardner and Lu (1991). In this case,
| 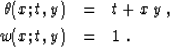 |
(2) |
| (3) |
Radon obtained a result similar to the theoretical inversion of
operator (1) with the summation path (2) and the
weighting function (3) in 1917, but this result was not
widely known until the development of computer tomography. According
to Radon 1917, the inverse operator has the form
| ![\begin{displaymath}
M(z,x) ={\bf A^{-1}}[S(t,y)]= \vert{\bf D}\vert^m\;\int
\widehat{w}\,S(\widehat{\theta}(y;z,x),y)\,dy\;,\end{displaymath}](img6.gif) |
(4) |
where
| 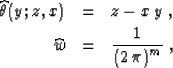 |
(5) |
| (6) |
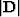 is a one-dimensional convolution operator with the
spectrum
is a one-dimensional convolution operator with the
spectrum 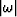 (the rho filter), and m is the
dimensionality of x and y (usually 1 or 2). In Russian
geophysical literature, a similar result for the inversion of the CDR
transform was published by Nakhamkin 1969.
(the rho filter), and m is the
dimensionality of x and y (usually 1 or 2). In Russian
geophysical literature, a similar result for the inversion of the CDR
transform was published by Nakhamkin 1969.
Extension of Radon's result to the general form of integral operator
(1) (generalized Radon transform) is
possible through asymptotic analysis of the inverse problem. In the
general case, it was shown Beylkin (1985); Goldin (1988) that asymptotic
inversion can reconstruct discontinuous parts of the model. These are
the parts responsible for the asymptotic behavior of the model at high
frequencies. Since the discontinuities are associated with wavefronts
and reflection events at seismic sections, there is a certain
correspondence between asymptotic inversion and such standard goals of
seismic data processing as kinematic equivalence and amplitude
preservation.
The main theorem of asymptotic inversion can be formulated as follows
Goldin (1988). Main (leading-order) discontinuities in M are
reconstructed by an integral operator of the form
| ![\begin{displaymath}
\widehat{M}(z,x)={\bf \widehat{A}}[S(t,y)]=
\vert{\bf D}\vert^m\;\int \widehat{w}(y;z,x)\,S(\widehat{\theta}(y;z,x),y)\;dy\;,\end{displaymath}](img10.gif) |
(7) |
where the summation path 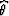 is obtained simply by
solving the equation
is obtained simply by
solving the equation
| 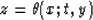 |
(8) |
for t (if such an explicit solution is possible). The correctly
chosen summation path reconstructs the geometry of the
discontinuities. To recover the amplitude, we must choose the correct
weighting function, which is constrained by the equation
| 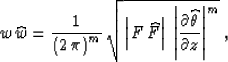 |
(9) |
where
| 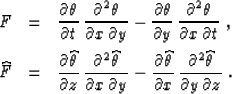 |
(10) |
| (11) |
The solution assumes that differential forms F and 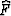 exist and are bounded and non-vanishing. In the multi-dimensional case
exist and are bounded and non-vanishing. In the multi-dimensional case
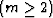 , they are replaced by the determinants of the
corresponding matrices. To ensure the asymptotic inversion, equation
(9) must be satisfied at least in the vicinity of the
stationary points of integral (1). Those are the points
where the summation path of the form (8) is tangent to the
traveltimes of the actual events on the transformed model.
, they are replaced by the determinants of the
corresponding matrices. To ensure the asymptotic inversion, equation
(9) must be satisfied at least in the vicinity of the
stationary points of integral (1). Those are the points
where the summation path of the form (8) is tangent to the
traveltimes of the actual events on the transformed model.
In the case of the Radon transform,
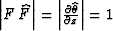 , and the asymptotic inverse coincides with the
exact inversion.
, and the asymptotic inverse coincides with the
exact inversion.





Next: PULL ADJOINTS
Up: Fomel: Stacking operators
Previous: THEORETICAL DEFINITION OF A
Stanford Exploration Project
9/11/2000
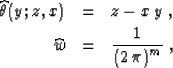
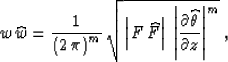
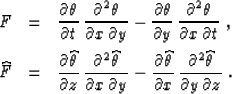
![]() , and the asymptotic inverse coincides with the
exact inversion.
, and the asymptotic inverse coincides with the
exact inversion.