




Next: ASYMPTOTIC INVERSION: RECONSTRUCTING THE
Up: Fomel: Stacking operators
Previous: Introduction
In practice, integration of discrete data is performed by stacking,
which requires special caution in the case of spatial aliasing
Claerbout (1992). In theory, it is convenient to
represent a stacking operator in the form of a continuous integral:
| ![\begin{displaymath}
S(t,y)= {\bf A}\left[M(z,x)\right]=
\int w(x;t,y)\,M(\theta(x;t,y),x)\,dx\;.\end{displaymath}](img1.gif) |
(1) |
Function M(z,x) is the input of the operator, S(t,y) is the
output, 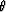 represents the summation path, and w stands for the
weighting function. The range of integration (the
operator aperture) may also depend on t and y. Allowing x to be
a two-dimensional variable, we can use definition (1) to
represent an operator applied to three-dimensional data. Throughout
this paper, I assume that t and z belong to a one-dimensional
space, and that x and y have the same number of dimensions.
represents the summation path, and w stands for the
weighting function. The range of integration (the
operator aperture) may also depend on t and y. Allowing x to be
a two-dimensional variable, we can use definition (1) to
represent an operator applied to three-dimensional data. Throughout
this paper, I assume that t and z belong to a one-dimensional
space, and that x and y have the same number of dimensions.
The goal of inversion is to reconstruct some function
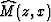 for a given S(t,y), so that
for a given S(t,y), so that 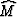 is in a
particular sense close to M in equation (1).
is in a
particular sense close to M in equation (1).





Next: ASYMPTOTIC INVERSION: RECONSTRUCTING THE
Up: Fomel: Stacking operators
Previous: Introduction
Stanford Exploration Project
9/11/2000
![]() for a given S(t,y), so that
for a given S(t,y), so that ![]() is in a
particular sense close to M in equation (1).
is in a
particular sense close to M in equation (1).