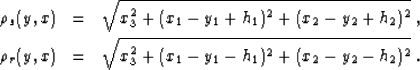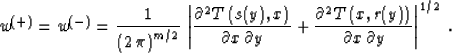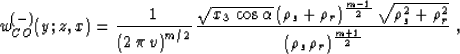Next: Post-Stack Time Migration
Up: EXAMPLES
Previous: Datuming
As recognized recently by Tygel et al. 1994,
true-amplitude migration Goldin (1992); Schleicher et al. (1993) is the asymptotic inversion
of seismic modeling represented by the Kirchhoff high-frequency
approximation. The Kirchhoff approximation for a reflected wave
Bleistein (1984); Haddon and Buchen (1981) belongs to the class of stacking-type operators
(1) with the summation path
| 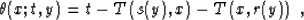 |
(45) |
the weighting function
| 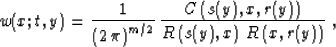 |
(46) |
and the additional time filter 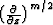 . Here x denotes a point at the reflector surface,
s is the source location, and r is the receiver location at the
observation surface. The parameter y corresponds to the
configuration of observation. That is,
. Here x denotes a point at the reflector surface,
s is the source location, and r is the receiver location at the
observation surface. The parameter y corresponds to the
configuration of observation. That is, 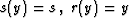 for the
common-shot configuration, s(y) = r(y) = y for the zero-offset
configuration, and
for the
common-shot configuration, s(y) = r(y) = y for the zero-offset
configuration, and 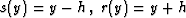 for the
common-offset configuration (where h is the half-offset). The
functions T and R have the same meaning as in the datuming example,
representing the one-way traveltime and the one-way geometric
spreading, respectively. The function C(s,x,r) is known as the
obliquity factor. Its definition is
for the
common-offset configuration (where h is the half-offset). The
functions T and R have the same meaning as in the datuming example,
representing the one-way traveltime and the one-way geometric
spreading, respectively. The function C(s,x,r) is known as the
obliquity factor. Its definition is
| 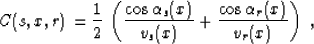 |
(47) |
where the angles 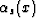 and
and 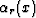 are formed by the
incident and reflected waves with the normal to the reflector at the
point x, and vs(x) and vr(x) are the corresponding velocities
in the vicinity of this point. In this paper, I leave the case of
converted (e.g., P-SV) waves outside the scope of consideration and
assume that vs(x) equals vr(x) (e.g., in P-P reflection). In this
case, it is important to notice that at the stationary point of the
Kirchhoff integral,
are formed by the
incident and reflected waves with the normal to the reflector at the
point x, and vs(x) and vr(x) are the corresponding velocities
in the vicinity of this point. In this paper, I leave the case of
converted (e.g., P-SV) waves outside the scope of consideration and
assume that vs(x) equals vr(x) (e.g., in P-P reflection). In this
case, it is important to notice that at the stationary point of the
Kirchhoff integral, 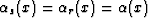 (the law of
reflection), and therefore
(the law of
reflection), and therefore
| 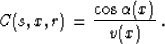 |
(48) |
The stationary point of the Kirchhoff integral is the point where the
stacking curve (45) is tangent to the actual reflection
traveltime curve. When our goal is asymptotic inversion, it is
appropriate to use equation (48) in place of
(47) to construct the inverse operator. The weighted
function (46) can include other factors affecting the
leading-order (WKBJ) ray amplitude, such as the source signature,
caustics counter (the KMAH-index), and transmission coefficient
for the interfaces Cerveny et al. (1977); Chapman and Drummond (1982). In the following analysis,
I neglect these factors for simplicity.
The model M implied by the Kirchhoff modeling integral is the
wavefield with the wavelet shape of the incident wave and the
amplitude proportional to the reflector coefficient along the
reflector surface. The goal of true-amplitude migration is to recover
M from the observed seismic data. In order to obtain the image of
the reflectors, the reconstructed model is evaluated at the time z
equal to zero. The Kirchhoff modeling integral requires explicit
definition of the reflector surface. However, its inverse doesn't
require explicit specification of the reflector location. For each
point of the subsurface, one can find the normal to the hypothetical
reflector by bisecting the angle between the s-x and x-r
rays. Born scattering approximation provides a different physical
model for the reflected waves. According to this approximation, the
recorded waves are viewed as scattered on smooth local inhomogeneities
rather than reflected from sharp reflector surfaces. The inversion of
Born modeling Bleistein (1987); Miller et al. (1987) closely
corresponds with the result of Kirchhoff integral inversion. For an
unknown reflector and the correct macro-velocity model, the asymptotic
inversion reconstructs the signal located at the reflector surface
with the amplitude proportional to the reflector coefficient.
As follows from the form of the summation path (45), the
integral migration operator must have the summation path
| 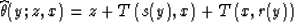 |
(49) |
to reconstruct the geometry of the reflector at the migrated
section. According to (7), the asymptotic reconstruction of the
wavelet requires, in addition, the derivative filter 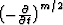 . The asymptotic reconstruction of
the amplitude defines the true-amplitude weighting function in
accordance with (9), as follows:
. The asymptotic reconstruction of
the amplitude defines the true-amplitude weighting function in
accordance with (9), as follows:
| 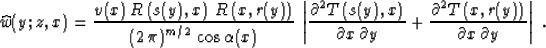 |
(50) |
In the case of common-shot migration, we can simplify equation (50)
with the help of Gritsenko's formula (39) to the form
| 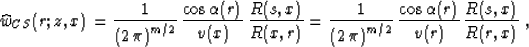 |
(51) |
where the angle 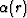 is measured between the reflected ray and
the normal to the observation surface at the reflector point
r. Formula (51) coincides with the analogous result of Keho
and Beydoun 1988, derived directly from
Claerbout's imaging principle Claerbout (1970). An alternative
derivation is given by Goldin 1987. Docherty
1991 points out a remarkable correspondence
between this formula and the classic results of Born scattering
inversion Bleistein (1987).
is measured between the reflected ray and
the normal to the observation surface at the reflector point
r. Formula (51) coincides with the analogous result of Keho
and Beydoun 1988, derived directly from
Claerbout's imaging principle Claerbout (1970). An alternative
derivation is given by Goldin 1987. Docherty
1991 points out a remarkable correspondence
between this formula and the classic results of Born scattering
inversion Bleistein (1987).
In the case of zero-offset migration, Gritsenko's formula
simplifies the true-amplitude migration weighting function
(50) to the form
| 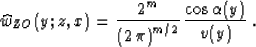 |
(52) |
In a constant-velocity medium, one can accomplish the true-amplitude
zero-offset migration by premultiplying the recorded zero-offset
seismic section by the factor 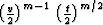 [which corresponds at the stationary point to the
geometric spreading R(x,y)] and downward continuation according to
formula (44) with the effective velocity v/2
Goldin (1987); Hubral et al. (1991). This conclusion is in
agreement with the analogous result of Born inversion
Bleistein et al. (1985), though derived from a different viewpoint.
[which corresponds at the stationary point to the
geometric spreading R(x,y)] and downward continuation according to
formula (44) with the effective velocity v/2
Goldin (1987); Hubral et al. (1991). This conclusion is in
agreement with the analogous result of Born inversion
Bleistein et al. (1985), though derived from a different viewpoint.
In the case of common-offset migration in a general variable-velocity
medium, the weighting function (50) cannot be simplified to a
different form, and all its components need to be calculated
explicitly by dynamic ray tracing Cerveny and de Castro (1993). In the
constant-velocity case, we can differentiate the explicit expression
for the summation path
| 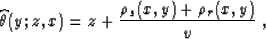 |
(53) |
where 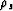 and
and
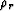 are the lengths of the incident and reflected rays:
are the lengths of the incident and reflected rays:
| 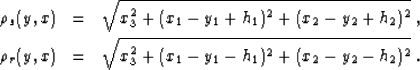 |
(54) |
| (55) |
For simplicity, the vertical component of the midpoint y3 is set here to zero. Evaluating the second derivative term in formula
(50) for the common-offset geometry leads, after some heavy
algebra, to the expression
| 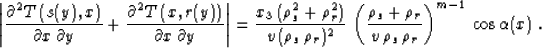 |
(56) |
Substituting (56) into the general formula (50) yields
the weighting function for the common-offset true-amplitude
constant-velocity migration:
| 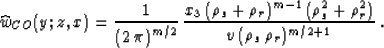 |
(57) |
Formula (57) is similar to the result obtained by Sullivan and
Cohen 1987. In the case of zero offset h=0,
(57) reduces to formula (52). Note that the value of m=1 in
(57) corresponds to the two-dimensional (cylindric) waves
recorded on the seismic line. A special case, valuable in practice, is
the 2.5-D inversion, when the waves are assumed to be spherical, while
the recording is on a line, and the medium has cylindric symmetry. In
this case, the modeling weighting function (46) transforms to
Bleistein (1986); Deregowski and Brown (1983)
| 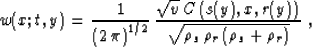 |
(58) |
and the time filter is 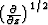 . Combining this result with formula (56)
for m=1, we obtain the weighting function for the 2.5-D
common-offset migration in a constant velocity medium
Sullivan and Cohen (1987):
. Combining this result with formula (56)
for m=1, we obtain the weighting function for the 2.5-D
common-offset migration in a constant velocity medium
Sullivan and Cohen (1987):
| 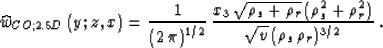 |
(59) |
The corresponding time filter for 2.5-D migration is 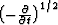 .
.
The weighting function of the asymptotic pseudo-unitary migration is found
analogously to (38) as
| 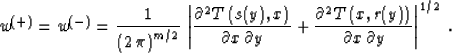 |
(60) |
Unlike true-amplitude migration, this type of migration operator
doesn't change the dimensionality of the input. For common-shot
migration, pseudo-unitary weighting coincides with the weighting of
datuming and corresponds to the downward continuation of the
receivers. In the zero-offset case, it reduces to downward
pseudo-unitary continuation with a velocity of v/2. In the
common-offset case, the pseudo-unitary weighting is defined from
(60) and (56) as follows:
| 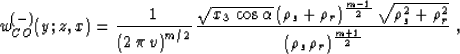 |
(61) |
where
| 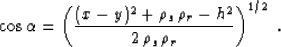 |
(62) |





Next: Post-Stack Time Migration
Up: EXAMPLES
Previous: Datuming
Stanford Exploration Project
9/11/2000