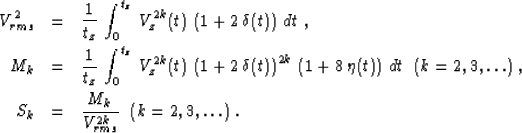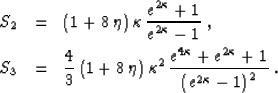Next: Stolt Stretch
Up: VERTICAL HETEROGENEITY
Previous: Isotropic Case
In a model that includes vertical heterogeneity and anisotropy, both
factors affect bending of the rays. However, the weak anisotropy
approximation allows us to neglect the effect of anisotropy on ray
trajectories and to consider its effect on traveltimes only. This
assumption is analogous to the linearization concept, conventional for
tomographic inversion. Its application to weak anisotropy has been
discussed by Grechka and McMechan 1996. According to
the linearization assumption, we can retain isotropic formula (24)
as describing the ray trajectories and rewrite formula (23) in the
form
| 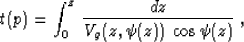 |
(43) |
where Vg is the anisotropic group velocity, which varies both with
depth and with the ray angle 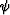 and has the expression
(1). Differentiation of the parametric traveltime formulas
(43) and (24) and linearization with respect to Thomsen's
anisotropic parameters shows that the general form of equations
(27) through (30) remains valid if we change the definition of the
root-mean-square velocity Vrms and the parameters S2 and
S3, as follows:
and has the expression
(1). Differentiation of the parametric traveltime formulas
(43) and (24) and linearization with respect to Thomsen's
anisotropic parameters shows that the general form of equations
(27) through (30) remains valid if we change the definition of the
root-mean-square velocity Vrms and the parameters S2 and
S3, as follows:
| 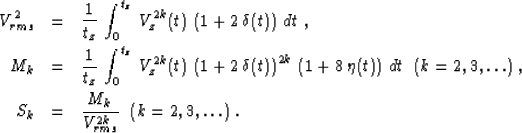 |
(44) |
| (45) |
| (46) |
It is easy to verify that in the homogeneous case, expressions
(44) through (46) transform series (26) with
coefficients (27) through (30) to the form equivalent to
series (17). Two important conclusions follow from the
mathematical form of equations (44) and (45). First, we
see that if the mean value of the anisotropic coefficient 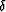 is
less than zero, the presence of anisotropy can reduce the difference
between the effective root-mean-square velocity and the effective
vertical velocity Vz=z/tz. In this case, the effects of anisotropy
and heterogeneity partially cancel each other, and the moveout curve
behaves at small offsets so as if the medium were homogeneous and
isotropic. This behavior has been noticed by Larner and Cohen
1993. On the other hand, if the anelliptic
parameter
is
less than zero, the presence of anisotropy can reduce the difference
between the effective root-mean-square velocity and the effective
vertical velocity Vz=z/tz. In this case, the effects of anisotropy
and heterogeneity partially cancel each other, and the moveout curve
behaves at small offsets so as if the medium were homogeneous and
isotropic. This behavior has been noticed by Larner and Cohen
1993. On the other hand, if the anelliptic
parameter  is positive and different from zero, it can
significantly increase the values of the heterogeneity parameters
Sk. In this case, the nonhyperbolicity of reflection moveouts at
large offsets is stronger than in the isotropic case.
is positive and different from zero, it can
significantly increase the values of the heterogeneity parameters
Sk. In this case, the nonhyperbolicity of reflection moveouts at
large offsets is stronger than in the isotropic case.
To exemplify the general theory, let us consider a simple analytic
model with constant anisotropy parameters and a vertical velocity
linearly increasing with depth according to the equation
| 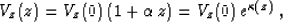 |
(47) |
where  is the logarithm of the velocity change. In this case,
the analytic expression for the RMS velocity Vrms is found
according to formula (44) to be
is the logarithm of the velocity change. In this case,
the analytic expression for the RMS velocity Vrms is found
according to formula (44) to be
| 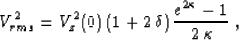 |
(48) |
while the mean vertical velocity is
| 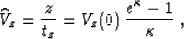 |
(49) |
where 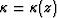 is evaluated at the reflector depth.
Comparing equations (48) and (49), we can see that
the squared RMS velocity Vrms2 equals the squared mean velocity
is evaluated at the reflector depth.
Comparing equations (48) and (49), we can see that
the squared RMS velocity Vrms2 equals the squared mean velocity
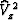 if
if
| 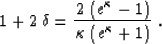 |
(50) |
For small  , the estimate of
, the estimate of 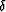 from equation
(50) is
from equation
(50) is
| 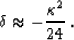 |
(51) |
For example, if the vertical velocity near the reflector is four times
higher than the velocity at the surface, having the anisotropic
parameter 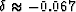 is sufficient to cancel out the
effect of heterogeneity on the normal moveout velocity. The values of
the parameters S2 and S3 are found from formula (46) to be
is sufficient to cancel out the
effect of heterogeneity on the normal moveout velocity. The values of
the parameters S2 and S3 are found from formula (46) to be
| 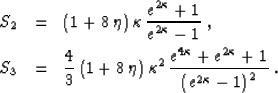 |
(52) |
| (53) |
Substituting (52) and (53) into formulas (35)
and (41) and linearizing both in  and in
and in  , we
find that the error of anisotropic traveltime approximation
(16) in the linear velocity model is approximately
, we
find that the error of anisotropic traveltime approximation
(16) in the linear velocity model is approximately
| 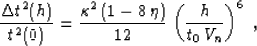 |
(54) |
while the error of the shifted hyperbola approximation
(33) is
| 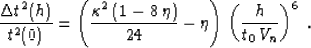 |
(55) |
Comparing formulas (54) and (55), we conclude
that if the medium is isotropic 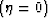 , the shifted hyperbola can
be twice as accurate as the anisotropic formula (assuming the optimal
choice of parameters). It is, however, less accurate if the
coefficient
, the shifted hyperbola can
be twice as accurate as the anisotropic formula (assuming the optimal
choice of parameters). It is, however, less accurate if the
coefficient  is positive and satisfies the approximate
inequality
is positive and satisfies the approximate
inequality
| 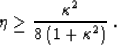 |
(56) |





Next: Stolt Stretch
Up: VERTICAL HETEROGENEITY
Previous: Isotropic Case
Stanford Exploration Project
9/12/2000