




Next: CURVILINEAR REFLECTOR
Up: VERTICAL HETEROGENEITY
Previous: Vertical Heterogeneity plus Anisotropy
Stolt stretch
Claerbout (1985); Levin (1985); Stolt (1978) is
a method of extending constant-velocity frequency-domain migration to
the case of a vertically variable velocity. The method consists of
stretching the time axis according to the formula
| 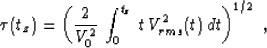 |
(57) |
double Fourier transform, and migration according to the dispersion
relation
| 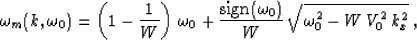 |
(58) |
where V0 is a constant frame velocity, 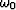 and
and 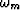 are the frequencies before and after the migration, corresponding to
the stretched time coordinate, kx is the wavenumber, and W is a
constant parameter (W=1 in the constant velocity case). Fomel
1995 has shown that the optimal choice of the
Stolt stretch parameter W for a particular traveltime depth tz is
given by the expression
are the frequencies before and after the migration, corresponding to
the stretched time coordinate, kx is the wavenumber, and W is a
constant parameter (W=1 in the constant velocity case). Fomel
1995 has shown that the optimal choice of the
Stolt stretch parameter W for a particular traveltime depth tz is
given by the expression
| 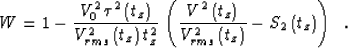 |
(59) |
This expression remains valid in the case of a vertically
heterogeneous VTI medium if the values
of Vrms and S2 are computed according to formulas (44)
and (46). The method of cascaded migrations
Larner and Beasley (1987) can improve the performance of Stolt
migration in the case of variable velocity
Beasley et al. (1988). However, this method affects only the
isotropic part of the model and cannot change the contribution of the
anisotropic parameters. Therefore, in the anisotropic case, it is
important to incorporate anisotropic parameters into the Stolt stretch
correction.





Next: CURVILINEAR REFLECTOR
Up: VERTICAL HETEROGENEITY
Previous: Vertical Heterogeneity plus Anisotropy
Stanford Exploration Project
9/12/2000