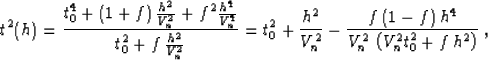Next: VERTICAL HETEROGENEITY
Up: Fomel & Grechka: Nonhyperbolic
Previous: WEAK ANISOTROPY APPROXIMATION
To exemplify the use of weak anisotropy, let us consider the
simplest case of a homogeneous anisotropic medium with a horizontal
reflector. In the isotropic case, the reflection traveltime curve is
an exact hyperbola, which follows directly from Pythagoras's theorem
(see Figure 2):
| 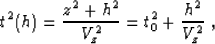 |
(13) |
where z denotes the depth of the reflector, h is the half-offset,
t0=t(0) is the zero-offset traveltime, and Vz corresponds to
half of the actual isotropic velocity. In the case of a homogeneous
VTI medium, the velocity Vz in formula (13) is replaced by
the angle-dependent group velocity Vg. This replacement leads to
the exact traveltimes, if no approximation for the group velocity is
used, since the ray trajectories in homogeneous VTI media remain
straight, and the reflection point does not shift because of the
vertical axis symmetry. We can also obtain an approximate
traveltime using the approximate velocity Vg defined in equation
(1) or (9). From the simple trigonometric considerations,
the ray angle 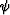 in this case is defined by the equation
in this case is defined by the equation
| 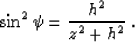 |
(14) |
Substituting equation (14) into (9) and linearizing the
expression
| 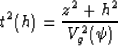 |
(15) |
with respect to anisotropic parameters 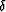 and
and  , we arrive
at the three-parameter nonhyperbolic approximation Tsvankin and Thomsen (1994)
, we arrive
at the three-parameter nonhyperbolic approximation Tsvankin and Thomsen (1994)
| 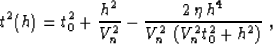 |
(16) |
where the normal moveout velocity Vn is defined by equation
(6). At small offsets 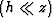 , the influence of the
parameter
, the influence of the
parameter  is negligible, and the traveltime curve is nearly
hyperbolic. At large offsets
is negligible, and the traveltime curve is nearly
hyperbolic. At large offsets 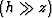 , the third term of equation
(16) has a clear influence on the behavior of the
traveltime. The Taylor series
expansion of formula (16) in the vicinity of the vertical
zero-offset ray has the form
, the third term of equation
(16) has a clear influence on the behavior of the
traveltime. The Taylor series
expansion of formula (16) in the vicinity of the vertical
zero-offset ray has the form
| 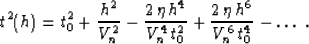 |
(17) |
When the offset h approaches infinity, the traveltime
approximately satisfies the intuitively reasonable relationship
| 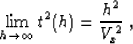 |
(18) |
where the horizontal velocity Vx is defined by
(5). Approximation (16) is analogous, within the weak
anisotropy assumption, to the ``skewed hyperbola'' formulas
Byun et al. (1989); Harlan (1995), which use the three velocities Vz,
Vn, and Vx as the parameters of the approximation, as follows:
| 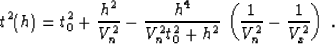 |
(19) |
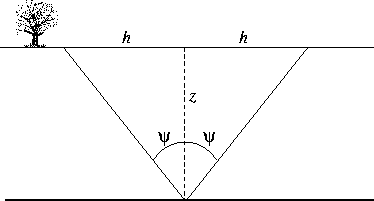
The accuracy of formula (16) for many realistic situation
lies within 1% error and can be further improved at a finite offset
by modifying the denominator of the third term Alkhalifah and Tsvankin (1995); Grechka and Tsvankin (1996).
nmoone
Figure 2 Reflected rays
in a homogeneous layer with a horizontal reflector (a scheme).

The anelliptic moveout approximation suggested by Muir and Dellinger
1985 has the form
| 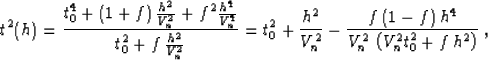 |
(20) |
where f is a dimensionless parameter of anellipticity. At large
offsets, formula (20) approaches
| 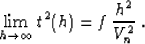 |
(21) |
Comparing equations (18) and (21), we can establish
the correspondence
| 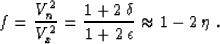 |
(22) |
Taking this correspondence into account, we can see that formula
(20) is approximately equivalent to formula (16)
in the sense that their difference has the order of  squared.
squared.





Next: VERTICAL HETEROGENEITY
Up: Fomel & Grechka: Nonhyperbolic
Previous: WEAK ANISOTROPY APPROXIMATION
Stanford Exploration Project
9/12/2000