Next: DISCUSSION
Up: Fomel & Claerbout: Galilee
Previous: FIRST RESULTS
A minor improvement in the method was the change from the Laplacian filter
(3) in equation (2) to the gradient filter consisting
of the two
orthogonal first-order derivatives
| 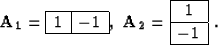 |
(4) |
The reason for this change is evident in Figure 5. The
gradient filter is more appropriate for the
sharp edges (the first-derivative jump) of the lake bottom, while the Laplacian
filter tends to smooth them out. This fact is related to the close
correspondence between gradient filter smoothing and local linear
interpolation on one side, and Laplacian smoothing and cubic (spline)
interpolation on the other.
The major enhancement is the introduction of a weighting operator
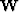 into
equation
(1). Thus system (1) - (2) takes the
form
into
equation
(1). Thus system (1) - (2) takes the
form
| 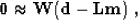 |
(5) |
| 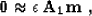 |
(6) |
| 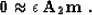 |
(7) |
Though we didn't apply any formal straightforward theory to choose the
weighting operator W, our heuristic choice followed two formal principles:
- 1.
- Bad (inconsistent) data points are indicated by large
values of the residual r = d - Lm left after conventional least squares
inversion.
- 2.
- Abnormally large residuals attract most of the conjugate
gradient solver's efforts, directing it the wrong way. The residual should be
whitened to distribute the solver's attention equally among all the
data points and emphasize the role of the ``consistent majority.''
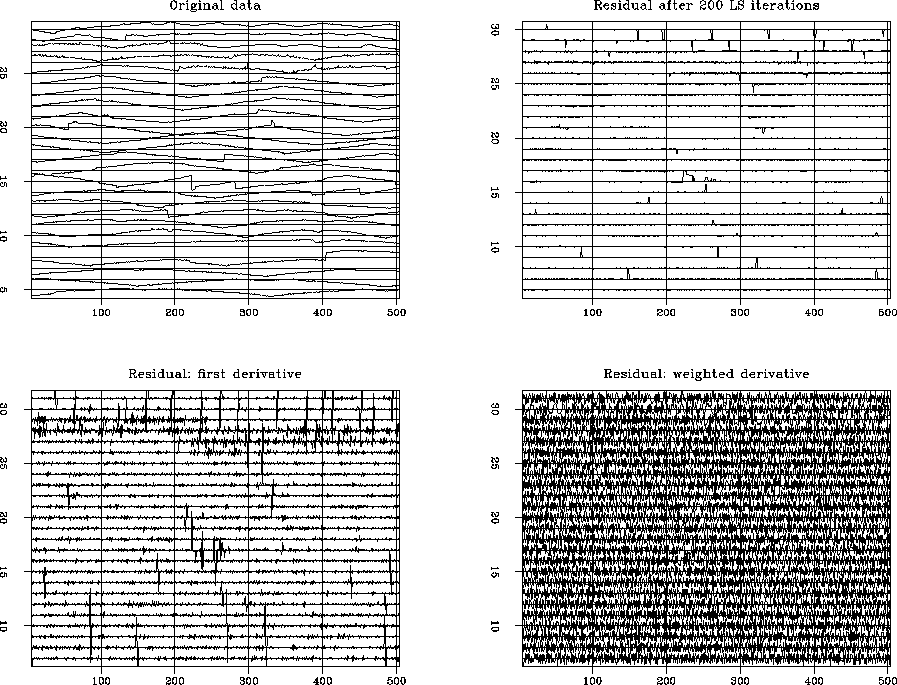
Figure 6 demonstrates changes in the residual space caused by
the weighting.
Each plot contains one long vector cut into several traces for better
viewing.
The top left plot is the original data
from the patch used in the first experiments. The top right plot is
the residual after 200
conventional conjugate gradient iterations. Note two major features of the
residual distribution: statically shifted tracks
(the zero-frequency
component) and local bursts of energy (mostly in the upper part of the
plot). To take away the zero-frequency component, we convolved the
residual with
the first-derivative operator. The result of differentiation appears on the
bottom left plot.
Finally, to take into account both large spikes created by differentiation and
local bursts of energy, we constructed the following weighting function:
| 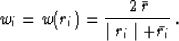 |
(8) |
Here 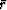 stands for the median of the absolute
residual values from the whole data set, and
stands for the median of the absolute
residual values from the whole data set, and 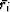 is the
median in a
small window around a current point ri. The denominator of the weighting
function is designed to reduce the value of the residual if it belongs
either to
a spike (large
is the
median in a
small window around a current point ri. The denominator of the weighting
function is designed to reduce the value of the residual if it belongs
either to
a spike (large 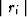 ) or to a local burst of energy (large
) or to a local burst of energy (large
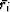 ). The numerator was chosen for scaling purposes. The
bottom right plot in Figure
6 justifies our choice of the weighting function, displaying the
residual derivative after weighting. The signal distribution resembles white
noise in accordance with the second formal principle.
galdat
). The numerator was chosen for scaling purposes. The
bottom right plot in Figure
6 justifies our choice of the weighting function, displaying the
residual derivative after weighting. The signal distribution resembles white
noise in accordance with the second formal principle.
galdat
Figure 6 View from the data space
(explanation in the text).





Thus the weighting operator 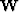 in equation (5) includes two
components: the first-derivative filter
in equation (5) includes two
components: the first-derivative filter 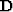 taken in the data space
along the recording tracks and the weighting function w. Since w
depends upon the residual, the inversion problem becomes nonlinear,
and the algorithm approaches the IRLS class Scales et al. (1988).
taken in the data space
along the recording tracks and the weighting function w. Since w
depends upon the residual, the inversion problem becomes nonlinear,
and the algorithm approaches the IRLS class Scales et al. (1988).
The result of the IRLS inversion is shown in Figure
7. While the noisy
portions of the model disappeared as we had
expected, a large-scale structure (valley) crossing the lake from north to
south remained on the image.
Comparison of Figures
9 and 10 demonstrates that the price for that
improvement is a certain loss in the
image resolution. This type of loss occurs because we rely on the
model smoothing to remove the noise influence. The role of the smoothing
increases when we apply IRLS in the manner of piece-wise
linearization. The first step of the piece-wise linear algorithm is
the conventional least squares minimization. The next step consists of
reweighted least squares iterations made in several cycles with reweighting
applied only at the beginning of each cycle. Thus the problem is linearized
within a cycle, and the conjugate gradient solver opens each cycle with the
steepest descent iteration.
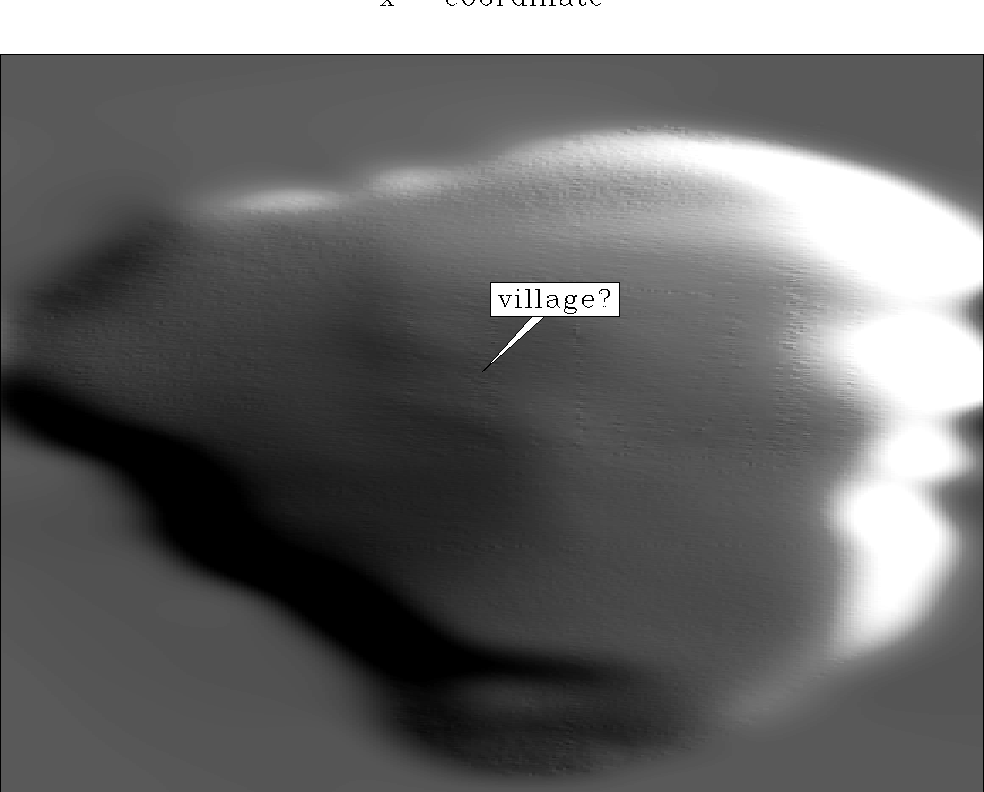
What happens when the nonlinear reweighting is applied on each
iteration is shown in Figure 8. Round
``villages'' on the bottom of the lake were identified as the
consequence of
occasional erroneous data points.
galrep
Figure 7 Result of the
IRLS inverse interpolation (piece-wise linear).




 galres
galres
Figure 8 Result of the
IRLS inverse interpolation (nonlinear).










Next: DISCUSSION
Up: Fomel & Claerbout: Galilee
Previous: FIRST RESULTS
Stanford Exploration Project
9/11/2000
![]() into
equation
(1). Thus system (1) - (2) takes the
form
into
equation
(1). Thus system (1) - (2) takes the
form
![]() in equation (5) includes two
components: the first-derivative filter
in equation (5) includes two
components: the first-derivative filter ![]() taken in the data space
along the recording tracks and the weighting function w. Since w
depends upon the residual, the inversion problem becomes nonlinear,
and the algorithm approaches the IRLS class Scales et al. (1988).
taken in the data space
along the recording tracks and the weighting function w. Since w
depends upon the residual, the inversion problem becomes nonlinear,
and the algorithm approaches the IRLS class Scales et al. (1988).