




Next: REFERENCES
Up: Fomel & Claerbout: Galilee
Previous: ENHANCEMENTS OF THE METHOD:
The method of inverse linear interpolation with IRLS enhancement was able to
produce a fairly clear image of the Sea of Galilee bottom, showing large-scale,
presumably geological structures. The lessons learned from the
Sea of Galilee project include the following:
- If a model (interpolation result) contains sharp edges, it can
be preferable to use a gradient filter instead of a Laplacian one for
smoothing purposes.
- The iteratively
reweighted least-squares approach is capable of removing non-Gaussian noise
influence on the result of inversion.
- The conjugate-gradient solver can behave differently in nonlinear and piece-wise linear implementations of nonlinear problems.
The main cause of the regular noise in the Galilee data set is
the inconsistency among repeated measurements. An
alternative approach could be applied to the problem
of the data track inconsistencies. A well-known
example of such an approach is the seismic mis-tie resolution
technique Harper (1991). Combining a technique of this
kind with the
inverse linear interpolation is a possible direction for
future research.
Another interesting
untested opportunity is preconditioning. As Bill Harlan has pointed out,
the two equations in the system (1) - (2)
contradict each other,
since the first one aims to build details in the model, while
the second tries to smooth them out. Applying the model
preconditioning method could change the contradictory
nature of the algorithm and speed up its convergence.
The inversion problem takes the form
| 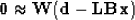 |
(9) |
| 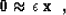 |
(10) |
where 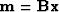 , and
, and 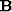 is a smoothing operator (an approximate
inverse of the roughening operator
is a smoothing operator (an approximate
inverse of the roughening operator 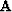 in (2)).
Possible advantages of preconditioning
deserve special investigation.
galavl
in (2)).
Possible advantages of preconditioning
deserve special investigation.
galavl
Figure 9 Result of the
LS inverse interpolation plotted in AVS.
 galavn
galavn
Figure 10 Result of the
IRLS inverse interpolation plotted in AVS.






Next: REFERENCES
Up: Fomel & Claerbout: Galilee
Previous: ENHANCEMENTS OF THE METHOD:
Stanford Exploration Project
9/11/2000

