 |
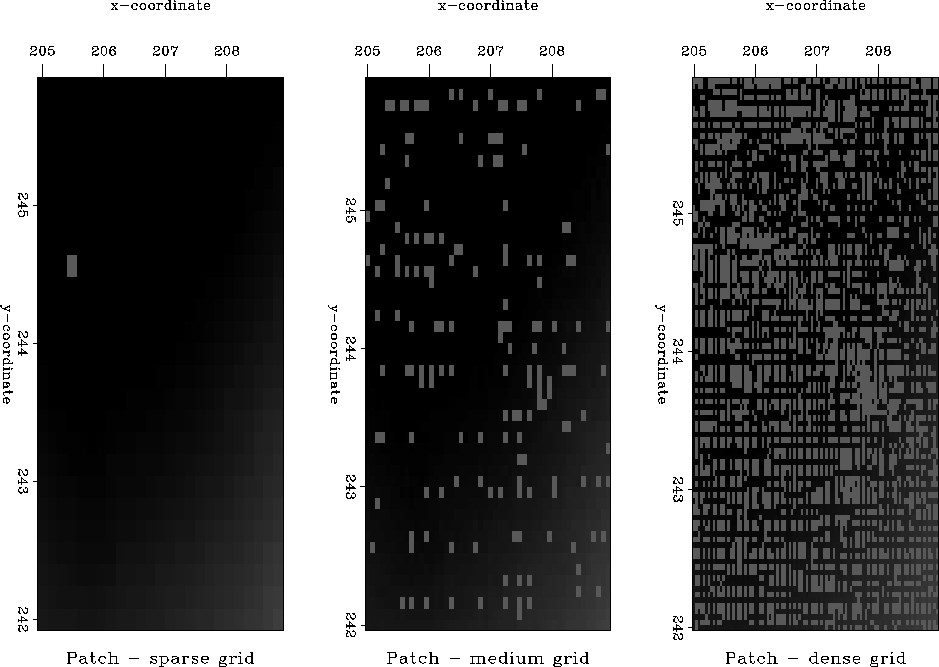
Figure 3 Simple binning of a patch. The left plot is the result of binning on a sparse grid (the size of a bin is 160 by 160 m); the right, on a denser grid (
To test the inverse linear interpolation method, we cut a 4 by 4 km patch from the initial data plane and posed the problem of interpolating the data to a regular mesh. Figure 3 shows the patch after sparse, medium, and dense simple binning.
 |
The result of the inverse linear interpolation on the dense grid after 200 iterations is shown in Figure 4. For a better display, we convolve the interpolated data with a set of first-order derivatives, taken in different directions, such as:
 |
The result looks encouraging, since the interpolation produced a more detailed image than simple binning. However, this image is not satisfactory. Studying the sharp dipping discontinuity in the upper-right quarter of the patch revealed that it was produced not by a real geological structure but by an inconsistent track present in the data. The results of applying the interpolation technique to the whole lake bottom (the left side of Figure 5) show more examples of that kind of noise and demonstrate that the problem of data inconsistency among different tracks is common for most parts of the lake.
Such an inconsistency is easily explained by taking into account the fact that the measurements were made on different days with different weather and human conditions. To allow for these circumstances, we had to reformulate the initial least squares optimization approach applied to inversion.
 |