




Next: The specular reflection coefficient
Up: THEORY
Previous: The reflected wavefield
Now that expressions for the incident and reflected vector wavefields have
been obtained in (21) and (24), the least-squares estimation of
the 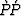 specular reflection coefficient can be evaluated
from (10):
specular reflection coefficient can be evaluated
from (10):
| 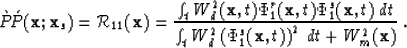 |
(26) |
First, the incident wave scalar can be evaluated given (5) and
(21):
| 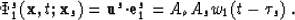 |
(27) |
Next, the reflected wave scalar can be evaluated given (5),
(24) and (25):
| ![\begin{displaymath}
\Phi^r_1({\bf x},t;{\bf x}_r) = \u^r{\bf \cdot}{\bf e}_1^r =...
...{\bf \cdot}(\nabla\u){\bf \cdot}{\bf n}'\right]\right\}\,dS'\;.\end{displaymath}](img108.gif) |
(28) |
Note that (28) requires knowledge of 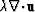 , the local
normal stress of the displacement field at each receiver, and
, the local
normal stress of the displacement field at each receiver, and
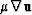 , the local stress tensor at each receiver.
For marine seismic data, the pressure
, the local stress tensor at each receiver.
For marine seismic data, the pressure 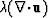 is measured
directly by hydrophones. However, for both land and marine data acquisition,
the local receiver stress tensor is not routinely measured.
As suggested by Keho (1986), I use a farfield WKBJ approximation of
the displacement vector wavefield gradient and divergence terms such that
is measured
directly by hydrophones. However, for both land and marine data acquisition,
the local receiver stress tensor is not routinely measured.
As suggested by Keho (1986), I use a farfield WKBJ approximation of
the displacement vector wavefield gradient and divergence terms such that
| 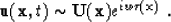 |
(29) |
Then
| 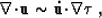 |
(30) |
and
| 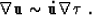 |
(31) |
In this case, (28) can be approximated for land acquisition as:
| ![\begin{displaymath}
\Phi^r_1({\bf x},t;{\bf x}_r) =
\int_{S'} A_r \left\{ \lam...
...dot{\u}}\nabla\tau_r){\bf \cdot}{\bf n}'\right]\right\}\,dS'\;.\end{displaymath}](img115.gif) |
(32) |
Substituting (27) and (32) into (26) and performing
the t integrations, one obtains
| 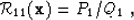 |
(33) |
such that
| ![\begin{eqnarray}
\lefteqn{P_1 =} \nonumber \\ & A_o A_s W_d^2({\bf x},\tau_s)
...
...u}}(t_{sr})\nabla\tau_r){\bf \cdot}{\bf n}'\right]\right\}\,dS'\;,\end{eqnarray}](img117.gif) |
|
| (34) |
where 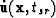 is now evaluated at the total ray traveltime
is now evaluated at the total ray traveltime
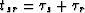 from each source at
from each source at 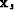 to any subsurface point
to any subsurface point
 and back up to each receiver position
and back up to each receiver position 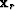 . The primed coordinates
indicate that the polarization vectors should be evaluated at the
receiver positions
. The primed coordinates
indicate that the polarization vectors should be evaluated at the
receiver positions 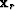 . The subscripts on
. The subscripts on
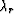 and
and 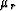 indicate that the Lamé parameters should be
evaluated at the receiver positions
indicate that the Lamé parameters should be
evaluated at the receiver positions 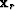 . Note that the
. Note that the  symbol
signifies a convolution of the surface data
symbol
signifies a convolution of the surface data  with the estimated
P-wave source wavelet w1.
The autocorrelation integral is
with the estimated
P-wave source wavelet w1.
The autocorrelation integral is
| 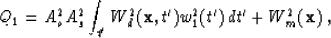 |
(35) |
and is related to the energy of the incident P wavefield.
Combining (33)-(35) yields:
| 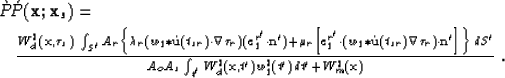 |
|
| (36) |
Equation (36) gives the least-squares
elastic wavefield integral solution for 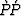 specular reflectivity. It can
be slightly simplified further by noting that
specular reflectivity. It can
be slightly simplified further by noting that
| 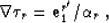 |
(37) |
which follows from the P-wave eikonal equation in (15),
where 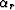 is the
P-wave velocity evaluated at each receiver location
is the
P-wave velocity evaluated at each receiver location 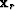 .
.





Next: The specular reflection coefficient
Up: THEORY
Previous: The reflected wavefield
Stanford Exploration Project
11/17/1997
![]() specular reflection coefficient can be evaluated
from (10):
specular reflection coefficient can be evaluated
from (10):
![]() , the local
normal stress of the displacement field at each receiver, and
, the local
normal stress of the displacement field at each receiver, and
![]() , the local stress tensor at each receiver.
For marine seismic data, the pressure
, the local stress tensor at each receiver.
For marine seismic data, the pressure ![]() is measured
directly by hydrophones. However, for both land and marine data acquisition,
the local receiver stress tensor is not routinely measured.
As suggested by Keho (1986), I use a farfield WKBJ approximation of
the displacement vector wavefield gradient and divergence terms such that
is measured
directly by hydrophones. However, for both land and marine data acquisition,
the local receiver stress tensor is not routinely measured.
As suggested by Keho (1986), I use a farfield WKBJ approximation of
the displacement vector wavefield gradient and divergence terms such that
![]() is now evaluated at the total ray traveltime
is now evaluated at the total ray traveltime
![]() from each source at
from each source at ![]() to any subsurface point
to any subsurface point
![]() and back up to each receiver position
and back up to each receiver position ![]() . The primed coordinates
indicate that the polarization vectors should be evaluated at the
receiver positions
. The primed coordinates
indicate that the polarization vectors should be evaluated at the
receiver positions ![]() . The subscripts on
. The subscripts on
![]() and
and ![]() indicate that the Lamé parameters should be
evaluated at the receiver positions
indicate that the Lamé parameters should be
evaluated at the receiver positions ![]() . Note that the
. Note that the ![]() symbol
signifies a convolution of the surface data
symbol
signifies a convolution of the surface data ![]() with the estimated
P-wave source wavelet w1.
The autocorrelation integral is
with the estimated
P-wave source wavelet w1.
The autocorrelation integral is
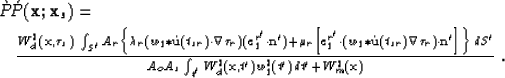
![]() specular reflectivity. It can
be slightly simplified further by noting that
specular reflectivity. It can
be slightly simplified further by noting that
![]() is the
P-wave velocity evaluated at each receiver location
is the
P-wave velocity evaluated at each receiver location ![]() .
.