The reflected wavefield

An expression for the reflected wavefield $\u^r({\bf x},t)$ can be obtained from the surface integrals of the general representation theorem (12):

 

$$\u^r({\bf x},t) = \int_{t'}\int_{S'} {\bf {\cal G}}^{T\ast... ...bla'\u({\bf x}',t')\right]\;{\bf \cdot}\;{\bf n}'\; dS' dt' \;,$$ (22)

in which I have assumed a free-surface boundary condition, such that the traction $({\bf {\cal C}}{\bf :}\nabla{\bf {\cal G}}){\bf \cdot}{\bf n}$ vanishes on S. Since the reconstruction of the subsurface reflected wavefield requires reverse time propagation, the conjugate $G^{\ast}$ is used. Using the WKBJ form (14), with ${\bf e}_k^n = {\bf e}_k^r$, the conjugate transpose Green's function can be evaluated as:

$$\begin{eqnarray} \lefteqn{{\bf {\cal G}}^{T\ast}({\bf x},t;{\bf x}',t') \sim } \... ...2^r{\bf e}_2^{r'}]^T + [{\bf e}_3^r{\bf e}_3^{r'}]^T\right) \;,\end{eqnarray}$$ (23)

where the primed polarization vectors ${\bf e}_k^{r'}$ are evaluated at the receiver positions ${\bf x}'={\bf x}_r$, and the unprimed polarization vectors ${\bf e}_k^r$are evaluated at the subsurface positions ${\bf x}$.Substituting (23) into (22) and performing the t' integration yields:

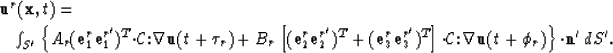$$\begin{eqnarray} \lefteqn{\u^r({\bf x},t) = } \nonumber \\ & \int_{S'} \left\{ A... ... C}}{\bf :} \nabla\u(t+\phi_r)\right\} {\bf \cdot}{\bf n}'\,dS' .\end{eqnarray}$$ (24)

In the case that the background propagation model is isotropic, which has been implicitly assumed in the definition of the Green's function (although this need not be the case), then the term ${\bf {\cal C}}{\bf :}\nabla\u$ can be written as

 

$${\bf {\cal C}}{\bf :}\nabla\u = \lambda\nabla{\bf \cdot}\u + \mu(\nabla\u + \u\nabla) \;,$$ (25)

where $\lambda({\bf x})$ and $\mu({\bf x})$ are the Lamé parameters. Thus, the solution for the reconstructed reflected vector wavefield $\u^r({\bf x},t)$in an isotropic ray-valid heterogeneous background medium is given by the surface integral (24) and the constitutive equation (25).