Consider a point ![]() in the subsurface. I define
the reflectivity matrix
in the subsurface. I define
the reflectivity matrix ![]() at the point
at the point ![]() by the following
relation between the incident displacement vector field
by the following
relation between the incident displacement vector field ![]() due
to a source at
due
to a source at ![]() , and the reflected displacement vector field
, and the reflected displacement vector field
![]() due to a receiver at the position
due to a receiver at the position ![]() :
:
| |
(1) |
where all quantities are evaluated locally at the point ![]() .The reflectivity matrix
.The reflectivity matrix ![]() is of order (3x3) and, in general,
is a scattering matrix which relates
is of order (3x3) and, in general,
is a scattering matrix which relates ![]() to
to ![]() and
contains refractions, diffractions and reflections. However, by anticipating
that
and
contains refractions, diffractions and reflections. However, by anticipating
that ![]() will be simulated as a direct primary incident field, and
will be simulated as a direct primary incident field, and
![]() will be reconstructed from refraction-muted surface observations as
a single-conversion primary reflected field, the interpretation of
will be reconstructed from refraction-muted surface observations as
a single-conversion primary reflected field, the interpretation of ![]() as
a generalized reflectivity matrix is justified.
as
a generalized reflectivity matrix is justified.
Now consider the local plane-wave unit
polarization vectors ![]() , where
, where ![]() is the local
P-wave propagation direction,
is the local
P-wave propagation direction, ![]() the S1 direction,
and
the S1 direction,
and ![]() the S2 direction. The displacement vectors
the S2 direction. The displacement vectors ![]() can
be expressed in this same ray-centered coordinate system without loss
of generality:
can
be expressed in this same ray-centered coordinate system without loss
of generality:
![]()
where u1 is the P-wave displacement amplitude, u2 is the S1
displacement amplitude, and u3 is the S2 displacement amplitude.
In this local ray-coordinate frame, the elements of ![]() are associated with
generalized non-specular elastic reflection coefficients:
are associated with
generalized non-specular elastic reflection coefficients:
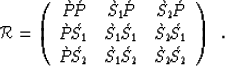 |
(2) |
The generalized non-specular reflection coefficients are related to
the plane-wave specular Zoeppritz coefficients as discussed by Frazer and Sen
(1985), and will be examined in more detail later in this paper.
It is apparent that the generalized reflection coefficients
within ![]() can be ``isolated'' by the appropriate vector dot products.
For example, the
can be ``isolated'' by the appropriate vector dot products.
For example, the ![]() coefficient can be isolated as
coefficient can be isolated as
| |
(3) |
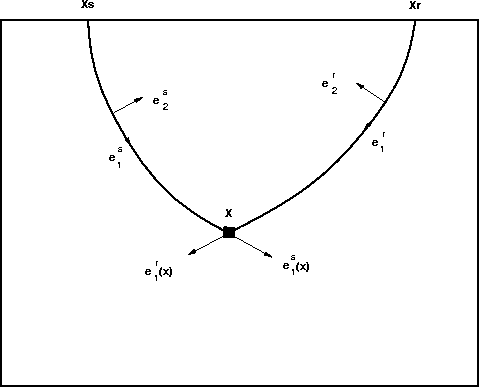
where ![]() is the local P-wave polarization vector of the incident
displacement vector
is the local P-wave polarization vector of the incident
displacement vector ![]() , evaluated at the subsurface point
, evaluated at the subsurface point ![]() ,
and
,
and ![]() is the
local P-wave polarization vector of the reflected displacement vector
is the
local P-wave polarization vector of the reflected displacement vector
![]() , evaluated at the subsurface point
, evaluated at the subsurface point ![]() .
Please refer to Figure
.
Please refer to Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to see the appropriate polarization vector geometry.
Similar dot product relations can be stated for the other
reflection coefficients
of
to see the appropriate polarization vector geometry.
Similar dot product relations can be stated for the other
reflection coefficients
of ![]() using the appropriate vector directions
using the appropriate vector directions ![]() .For example, the
.For example, the ![]() coefficient can be isolated as
coefficient can be isolated as
| |
(4) |
I will define the reflected scalar function on the left of (4)
as ![]() and the incident scalar function on the right of
(4) as
and the incident scalar function on the right of
(4) as ![]() :
:
![]()
| |
(5) |
 |
If I can forward model numerous source wavefields ![]() and I have numerous
reconstructions of the reflected wavefield
and I have numerous
reconstructions of the reflected wavefield ![]() from multiple
surface shot gather observations, then (5)
(and all of its nine converted-wave counterparts)
can be rearranged into an optimization problem to estimate
the isolated reflection coefficient, hereafter called
from multiple
surface shot gather observations, then (5)
(and all of its nine converted-wave counterparts)
can be rearranged into an optimization problem to estimate
the isolated reflection coefficient, hereafter called ![]() .
The objective function J for this problem has the general lp form
.
The objective function J for this problem has the general lp form
| |
(6) |
where Wd and Wm are arbitrary weighting functions in data and model
space respectively. The weighting functions in this form are nonconvolutional,
and therefore correspond to diagonal covariance functions ![]() in the
usual least-squares theory sense.
Note that adding the second term to (6)
will add stability to the final least-squares solution, and will ensure
that
in the
usual least-squares theory sense.
Note that adding the second term to (6)
will add stability to the final least-squares solution, and will ensure
that ![]() will be a minimum energy model in the lp sense, which is
appropriate for a desired spiky reflectivity solution.
Choosing the l2 norm and integrating over the
implicit functional dependencies, one obtains:
will be a minimum energy model in the lp sense, which is
appropriate for a desired spiky reflectivity solution.
Choosing the l2 norm and integrating over the
implicit functional dependencies, one obtains:
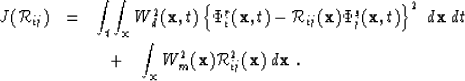 |
||
| (7) |
To extremize J and thus find an ``optimal'' solution for ![]() , I perform
the following stationary point analysis.
Perturb J by an arbitrary small amount
, I perform
the following stationary point analysis.
Perturb J by an arbitrary small amount ![]() :
:
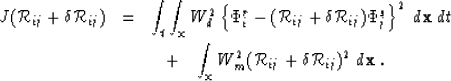 |
||
| (8) |
A stationary point of J with respect to ![]() occurs when
occurs when
![]()
Neglecting terms of order ![]() ,
,
| |
(9) |
Since ![]() is arbitrary, then the integrand kernel
is arbitrary, then the integrand kernel ![]() must vanish at the stationary point. This results in a least-squares
reflectivity solution:
must vanish at the stationary point. This results in a least-squares
reflectivity solution:
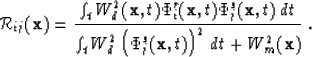 |
(10) |
Equation (10) is a weighted zero-lag correlation of the incident
and reflected wavefield scalar products, normalized by the weighted
minimum-threshold energy of the incident wavefield scalar product. Equation
(10) is valid for all of the generalized elastic reflection coefficients
of (2) by simply making the appropriate redefinitions of
![]() and
and ![]() as in (5).
as in (5).