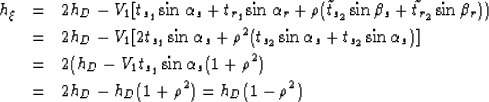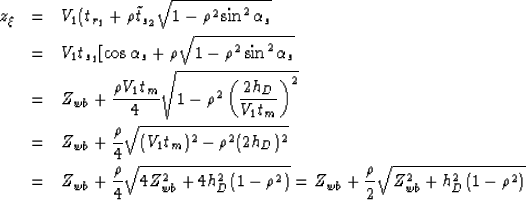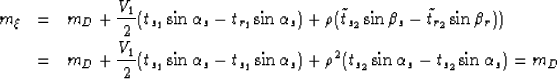Next: Computation of takeoff angles
Up: Alvarez: Multiples in image
Previous: Traveltime computations for dipping
In this Appendix, I show that the equations for the non-diffracted multiple
from a dipping water-bottom reduce to the equations for a flat water-bottom
when 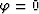 as they should. Setting
as they should. Setting 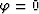 in
equations 39 through 42 we obtain
in
equations 39 through 42 we obtain
| 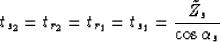 |
(66) |
and from equations 5 and 6 we get (as discussed at
the end of Appendix A) 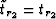 and
and 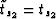 .Therefore,
.Therefore,
| 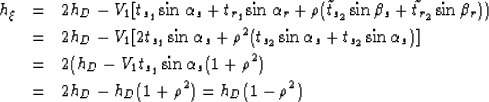 |
(67) |
| (68) |
| (69) |
| (70) |
Similarly,
| 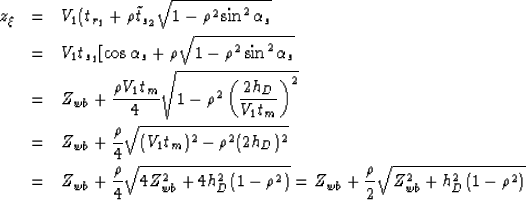 |
(71) |
| (72) |
| (73) |
| (74) |
| (75) |
Finally,
| 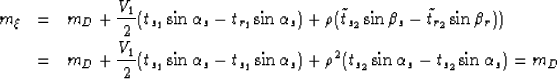 |
(76) |
| (77) |
E





Next: Computation of takeoff angles
Up: Alvarez: Multiples in image
Previous: Traveltime computations for dipping
Stanford Exploration Project
11/1/2005