




Next: From dip to no
Up: Alvarez: Multiples in image
Previous: Computation of Image Depth
In this Appendix I derive equations 39-45.
mul_sktch9
Figure 21 Sketch to show the computation
of ts1 and ts2 for a non-diffracted multiple from a dipping
water-bottom.
|
| 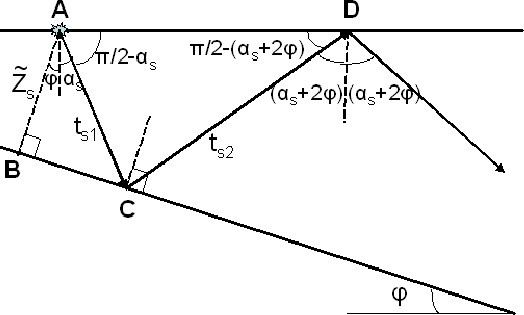 |

From triangle ABC in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we immediately get
we immediately get
| 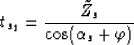 |
(57) |
and applying the law of sines to triangle ACD we get
| 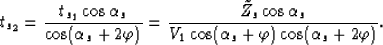 |
(58) |
mul_sktch10
Figure 22 Sketch to show the computation
of tr2 and tr1 for a non-diffracted multiple from a dipping
water-bottom.
|
| 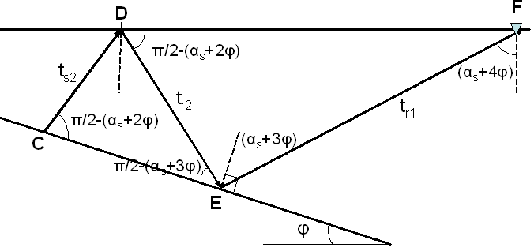 |

Similarly, repeated application of the law of sines to triangles CDE and DEF
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) gives
gives
| 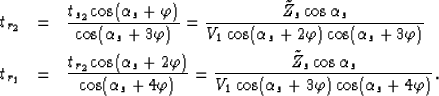 |
(59) |
| (60) |
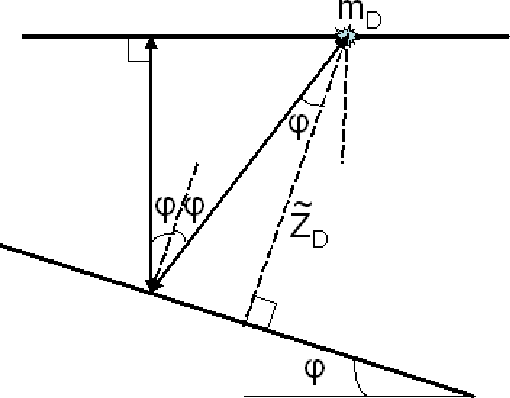
mul_sktch11
Figure 23 Sketch to show the computation
of 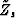 in equation 61. in equation 61.
|
| 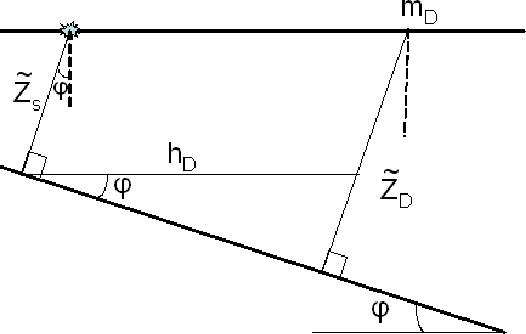 |

These equations are in terms of 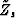 , which is not known. However,
from Figure
, which is not known. However,
from Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we see that
we see that
| 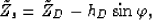 |
(61) |
and 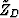 can be computed from the traveltime of the zero
surface-offset trace, since, according to Figure
can be computed from the traveltime of the zero
surface-offset trace, since, according to Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif)
| 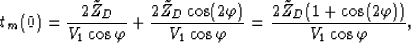 |
(62) |
from which it follows immediately that
| ![\begin{displaymath}
\tilde{Z}_D=\frac{V_1t_m(0)\cos\varphi}{2[1+\cos(2\varphi)]}.\end{displaymath}](img77.gif) |
(63) |
mul_sktch12
Figure 24 Sketch to show the computation
of 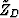 in equation 63. in equation 63.
|
|  |

Finally, we need to compute 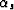 . Applying the law of sines to
triangle ABC in Figure
. Applying the law of sines to
triangle ABC in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we get
we get
| 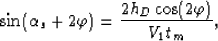 |
(64) |
from which we get
| ![\begin{displaymath}
\alpha_s=\sin^{-1}\left[\frac{2h_D\cos(2\varphi)}{V_1t_m}\right]-2\varphi.\end{displaymath}](img80.gif) |
(65) |
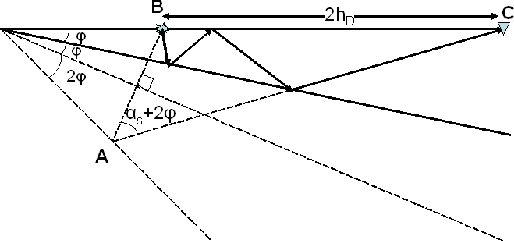
mul_sktch16
Figure 25 Sketch to compute
the takeoff angle of the source ray from a non-diffracted multiple
from a dipping water-bottom.
|
|  |

D





Next: From dip to no
Up: Alvarez: Multiples in image
Previous: Computation of Image Depth
Stanford Exploration Project
11/1/2005


![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we immediately get
we immediately get

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) gives
gives
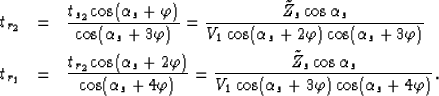

![]() , which is not known. However,
from Figure
, which is not known. However,
from Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we see that
we see that
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif)

![]() . Applying the law of sines to
triangle ABC in Figure
. Applying the law of sines to
triangle ABC in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we get
we get
