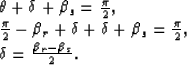Next: Traveltime computations for dipping
Up: Alvarez: Multiples in image
Previous: Computation of Traveltime for
mul_sktch17
Figure 20 Sketch to show the computation
of the image depth in an ADCIG.
|
| 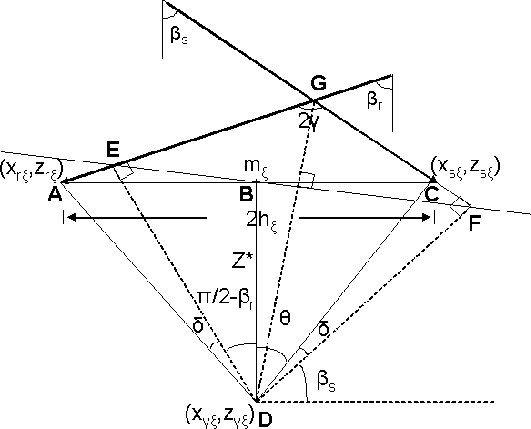 |

Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the basic construction to compute
the image depth in ADCIGs based on the image depth is SOCIGs. Triangles
ABD and CBD are congruent since they have one side common and the other
equal because |AB|=|BC|=
shows the basic construction to compute
the image depth in ADCIGs based on the image depth is SOCIGs. Triangles
ABD and CBD are congruent since they have one side common and the other
equal because |AB|=|BC|=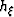 . Therefore,
. Therefore, 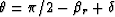 .
Also, triangles AED and FCD are congruent because |AD|=|CD| and also
|AE|=|CF| Biondi and Symes (2004). Therefore, the angle
.
Also, triangles AED and FCD are congruent because |AD|=|CD| and also
|AE|=|CF| Biondi and Symes (2004). Therefore, the angle 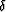 in triangle
DCF is the same as in triangle AED. We can compute
in triangle
DCF is the same as in triangle AED. We can compute 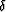 from the
condition
from the
condition
The depth of the image point in the ADCIG, from triangle ABC, is therefore
| 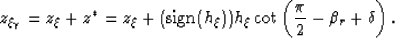 |
(55) |
Replacing the expression for 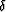 we get, after some simplification
(and taking sign
we get, after some simplification
(and taking sign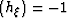 )
)
| 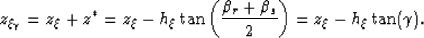 |
(56) |
C





Next: Traveltime computations for dipping
Up: Alvarez: Multiples in image
Previous: Computation of Traveltime for
Stanford Exploration Project
11/1/2005


![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the basic construction to compute
the image depth in ADCIGs based on the image depth is SOCIGs. Triangles
ABD and CBD are congruent since they have one side common and the other
equal because |AB|=|BC|=
shows the basic construction to compute
the image depth in ADCIGs based on the image depth is SOCIGs. Triangles
ABD and CBD are congruent since they have one side common and the other
equal because |AB|=|BC|=![]() . Therefore,
. Therefore, ![]() .
Also, triangles AED and FCD are congruent because |AD|=|CD| and also
|AE|=|CF| Biondi and Symes (2004). Therefore, the angle
.
Also, triangles AED and FCD are congruent because |AD|=|CD| and also
|AE|=|CF| Biondi and Symes (2004). Therefore, the angle ![]() in triangle
DCF is the same as in triangle AED. We can compute
in triangle
DCF is the same as in triangle AED. We can compute ![]() from the
condition
from the
condition