




Next: Diffracted multiple
Up: Dipping water-bottom
Previous: Dipping water-bottom
The water-bottom multiple from a dipping reflector has exactly the same
kinematics as a primary from a reflector with twice the dip
Alvarez (2005), that is,
| 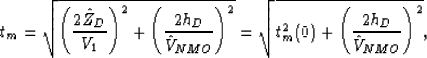 |
(31) |
where 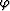 is the dip of the reflector,
is the dip of the reflector, 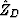 is the perpendicular
depth to the equivalent reflector with twice the dip (at the CMP location)
and
is the perpendicular
depth to the equivalent reflector with twice the dip (at the CMP location)
and 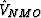 is the NMO velocity of the equivalent primary
is the NMO velocity of the equivalent primary
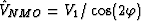 .
.
Following the same procedure as for the flat water-bottom, we compute
the coordinates of the image point using
equations 2-4 and noting that in this case
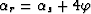 ,
,
| 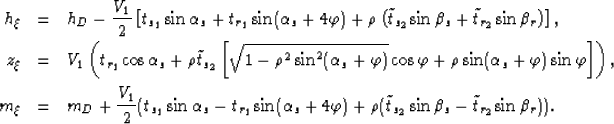 |
(32) |
| (33) |
| (34) |
where, according to equations 7-10,
| 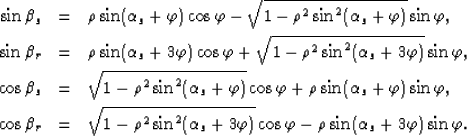 |
(35) |
| (36) |
| (37) |
| (38) |
The traveltimes of the individual ray segments are computed by
repeated application of the law of sines as shown in Appendix C:
| 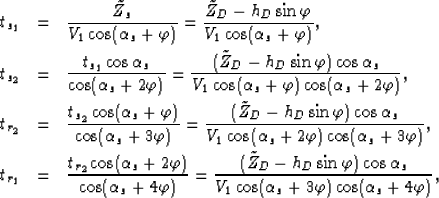 |
(39) |
| (40) |
| (41) |
| (42) |
where 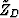 is the perpendicular depth to the reflector at the CMP
location and is given by (Appendix C):
is the perpendicular depth to the reflector at the CMP
location and is given by (Appendix C):
| ![\begin{displaymath}
\tilde{Z}_D=\frac{V_1t_m(0)\cos\varphi}{2[1+\cos(2\varphi)]}.\end{displaymath}](img77.gif) |
(43) |
Notice that this is not the same as 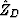 in equation 31,
which corresponds to the perpendicular depth to the equivalent reflector whose
primary has the same kinematics as the water-bottom multiple.
in equation 31,
which corresponds to the perpendicular depth to the equivalent reflector whose
primary has the same kinematics as the water-bottom multiple.
The traveltime of the refracted ray segments are given by
equations 5 and 6 with
| 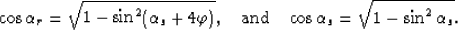 |
(44) |
In order for equation 32-34
to be useful in practice, we need to
express them entirely in terms of the known data coordinates, which means that
we need to find an expression for 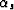 in terms of
in terms of
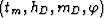 . In Appendix C it is shown that
. In Appendix C it is shown that
| ![\begin{displaymath}
\alpha_s=\sin^{-1}\left[\frac{2h_D\cos(2\varphi)}{V_1t_m}\right]-2\varphi.\end{displaymath}](img80.gif) |
(45) |
We now have all the pieces to compute the image space coordinates, since
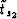 and
and 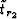 can be computed from
equations 5 and 6 using
equations 35-45.
can be computed from
equations 5 and 6 using
equations 35-45.
Appendix D shows that equations 32-34 reduce to the
corresponding equations for the non-diffracted multiple from a flat water
bottom when 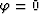 , as they should.
, as they should.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the zero subsurface offset section from a
migrated non-diffracted multiple from a dipping water-bottom. The overlaid
curve was computed with equations 32-34.
The dip of the water-bottom is 15 degrees and intercepts the surface at
CMP location zero. The CMP range of the data is from 2000 to 3000 m and
the surface offsets from 0 to 2000 m. The multiple was migrated with the
same two-layer model described before. Notice how the multiple was migrated
as a primary. Since the migration velocity is faster than water-velocity, the
multiple is over-migrated and appears much steeper and shallower than it
should (recall that it would be migrated as a reflector with twice the
dip is the migration velocity were that of the water.)
shows the zero subsurface offset section from a
migrated non-diffracted multiple from a dipping water-bottom. The overlaid
curve was computed with equations 32-34.
The dip of the water-bottom is 15 degrees and intercepts the surface at
CMP location zero. The CMP range of the data is from 2000 to 3000 m and
the surface offsets from 0 to 2000 m. The multiple was migrated with the
same two-layer model described before. Notice how the multiple was migrated
as a primary. Since the migration velocity is faster than water-velocity, the
multiple is over-migrated and appears much steeper and shallower than it
should (recall that it would be migrated as a reflector with twice the
dip is the migration velocity were that of the water.)
image3
Figure 11 image section at zero
subsurface offset for a non-diffracted multiple from a dipping water-bottom.
The overlaid curve was computed with equation 34
and 33.
|
|  |





Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the SODCIG at CMP 1500 m in i
Figure
shows the SODCIG at CMP 1500 m in i
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Just as for the flat water-bottom, the multiple
energy is mapped to negative subsurface offsets since
. Just as for the flat water-bottom, the multiple
energy is mapped to negative subsurface offsets since 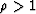 . The overlaid
curve is the moveout computed with equations 32-34.
. The overlaid
curve is the moveout computed with equations 32-34.
odcig3
Figure 12 SODCIG from a non-diffracted multiple
from a dipping water-bottom. The overlaid residual moveout curve was computed with equation 32 and 33.
|
|  |





The aperture angle is given by equation 11 with
| 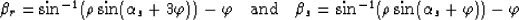 |
(46) |
and 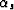 given by equation 45. The image depth in the
ADCIG is given by equation 12 with
given by equation 45. The image depth in the
ADCIG is given by equation 12 with 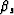 and
and 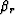 given
by equation 46 and
given
by equation 46 and 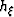 and
and 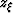 given by
equations 32 and 33. Figure
given by
equations 32 and 33. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the
ADCIG corresponding to the SODCIG in Figure
shows the
ADCIG corresponding to the SODCIG in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Notice that the
apex is at zero aperture angle.
. Notice that the
apex is at zero aperture angle.
adcig3
Figure 13 ADCIG corresponding to the SODCIG
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The overlaid residual moveout curve was
computed with equation 33, 11, 12,
and 46. . The overlaid residual moveout curve was
computed with equation 33, 11, 12,
and 46.
|
|  |










Next: Diffracted multiple
Up: Dipping water-bottom
Previous: Dipping water-bottom
Stanford Exploration Project
11/1/2005
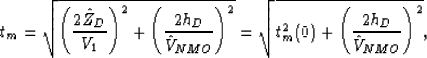
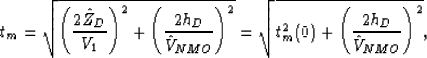
![]() ,
,
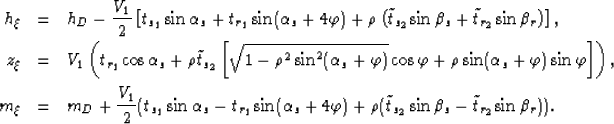
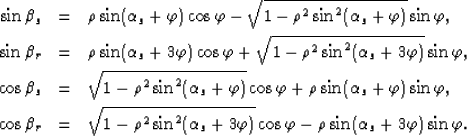
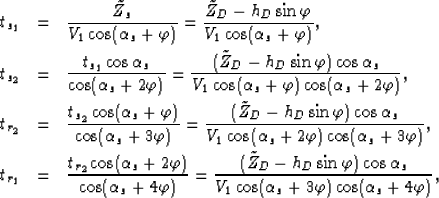
![]() , as they should.
, as they should.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the zero subsurface offset section from a
migrated non-diffracted multiple from a dipping water-bottom. The overlaid
curve was computed with equations 32-34.
The dip of the water-bottom is 15 degrees and intercepts the surface at
CMP location zero. The CMP range of the data is from 2000 to 3000 m and
the surface offsets from 0 to 2000 m. The multiple was migrated with the
same two-layer model described before. Notice how the multiple was migrated
as a primary. Since the migration velocity is faster than water-velocity, the
multiple is over-migrated and appears much steeper and shallower than it
should (recall that it would be migrated as a reflector with twice the
dip is the migration velocity were that of the water.)
shows the zero subsurface offset section from a
migrated non-diffracted multiple from a dipping water-bottom. The overlaid
curve was computed with equations 32-34.
The dip of the water-bottom is 15 degrees and intercepts the surface at
CMP location zero. The CMP range of the data is from 2000 to 3000 m and
the surface offsets from 0 to 2000 m. The multiple was migrated with the
same two-layer model described before. Notice how the multiple was migrated
as a primary. Since the migration velocity is faster than water-velocity, the
multiple is over-migrated and appears much steeper and shallower than it
should (recall that it would be migrated as a reflector with twice the
dip is the migration velocity were that of the water.)

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the SODCIG at CMP 1500 m in i
Figure
shows the SODCIG at CMP 1500 m in i
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Just as for the flat water-bottom, the multiple
energy is mapped to negative subsurface offsets since
. Just as for the flat water-bottom, the multiple
energy is mapped to negative subsurface offsets since ![]() . The overlaid
curve is the moveout computed with equations 32-34.
. The overlaid
curve is the moveout computed with equations 32-34.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the
ADCIG corresponding to the SODCIG in Figure
shows the
ADCIG corresponding to the SODCIG in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Notice that the
apex is at zero aperture angle.
. Notice that the
apex is at zero aperture angle.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The overlaid residual moveout curve was
computed with equation 33, 11, 12,
and 46.
. The overlaid residual moveout curve was
computed with equation 33, 11, 12,
and 46.
