




Next: Flat water-bottom
Up: Alvarez: Multiples in image
Previous: Introduction
mul_sktch1
Figure 1 Water-bottom multiple. The
subscript s refers to the source and the subscript r to the receiver.
|
| 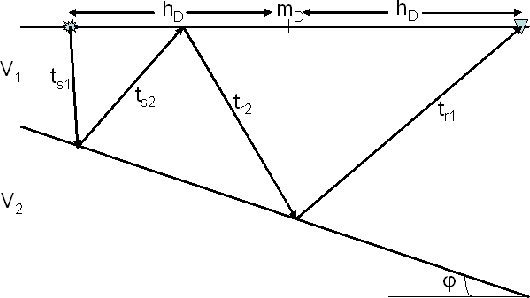 |

The propagation path of a water-bottom multiple, as shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , consists of four
segments, such that the total travel-time for the multiple is given by
, consists of four
segments, such that the total travel-time for the multiple is given by
where the subscript s refers to the source-side rays and the subscript
r refers to the receiver-side rays. The data space coordinates are
(mD,hD,tm) where mD is the horizontal position of the CMP gather
and hD is the half-offset between source and receiver.
Wave-equation migration maps
the CMP gathers to SODCIGs with coordinates 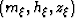 where
where
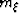 is the horizontal position of the image gather, and
is the horizontal position of the image gather, and
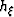 and
and 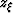 are the half subsurface-offset and the depth of the image,
respectively.
are the half subsurface-offset and the depth of the image,
respectively.
mul_sktch2
Figure 2 Imaging of water-bottom multiple
in SODCIG. The subscript 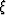 refers to the image point. refers to the image point.
|
| 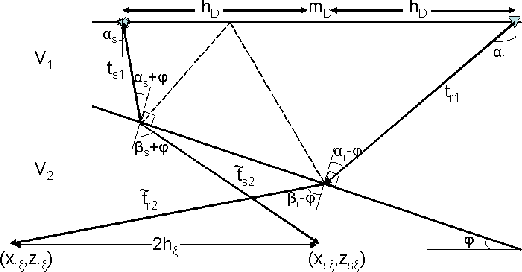 |

As illustrated in the sketch of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , at any given depth the image space coordinates
of the migrated multiple are given by:
, at any given depth the image space coordinates
of the migrated multiple are given by:
| 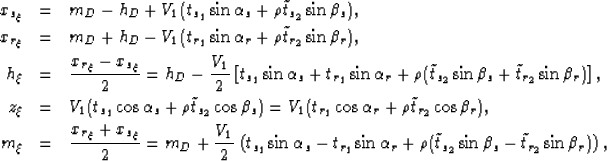 |
|
| |
| (2) |
| (3) |
| (4) |
where V1 is the water velocity, 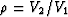 with V2 the sediment
velocity, and
with V2 the sediment
velocity, and 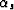 ,
, 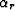 are the acute takeoff angles of the source
and receiver rays with respect to the vertical. The
traveltime of the refracted ray segments
are the acute takeoff angles of the source
and receiver rays with respect to the vertical. The
traveltime of the refracted ray segments 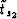 and
and 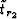 can be computed from two conditions: (1) at the image point the depth of
both rays has to be the same (since we are computing horizontal subsurface
offset gathers) and (2)
can be computed from two conditions: (1) at the image point the depth of
both rays has to be the same (since we are computing horizontal subsurface
offset gathers) and (2)
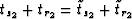 which follows immediately
from equation 1 since at the image point the extrapolated time
equals the traveltime of the multiple. As shown in Appendix A, the
traveltimes of the refracted rays are given by
which follows immediately
from equation 1 since at the image point the extrapolated time
equals the traveltime of the multiple. As shown in Appendix A, the
traveltimes of the refracted rays are given by
| 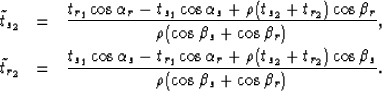 |
(5) |
| (6) |
The refracted angles are related to the takeoff angles by Snell's law:
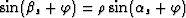 and
and
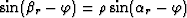 , from which we get
, from which we get
| 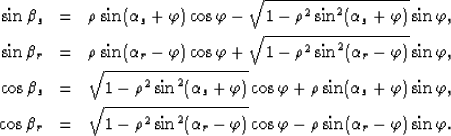 |
(7) |
| (8) |
| (9) |
| (10) |
Equations 2-10 are valid for any
water-bottom multiple, whether from
a flat or dipping water-bottom. They even describe the migration of
source- or receiver-side diffraction multiples, since no assumption has been
made relating 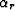 and
and 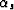 or the individual traveltime segments.
or the individual traveltime segments.
mul_sktch3
Figure 3 Imaging of water-bottom multiple
in ADCIG. The subscript 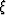 refers to the image point. The line AB represents
the apparent reflector at the image point. refers to the image point. The line AB represents
the apparent reflector at the image point.
|
| 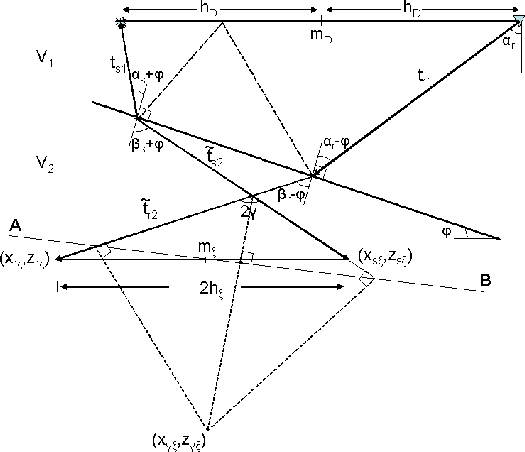 |

In ADCIGs, the mapping of the multiples can be directly related to the
previous equations by the geometry shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The half-aperture angle is given by
.
The half-aperture angle is given by
| 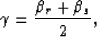 |
(11) |
which is the same equation used for converted waves
Rosales and Biondi (2005). The depth of the image point
(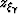 ) is given by (Appendix B)
) is given by (Appendix B)
| 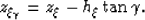 |
(12) |
Equations 2-12 formally describe the image
coordinates in terms of
the data coordinates. They are, however, of little practical use unless
we can relate the individual traveltime segments (ts1, ts2,
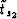 , tr2,
, tr2, 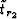 , tr1), and the
angles
, tr1), and the
angles 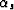 and
and 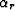 (which in turn determine
(which in turn determine 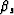 and
and
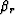 ) to the known data space
parameters (mD, hD, tm, V1,
) to the known data space
parameters (mD, hD, tm, V1, 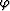 and
and 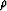 ). This may not be easy or
even possible analytically for all situations, but it is for some simple
but important models that I will now examine.
). This may not be easy or
even possible analytically for all situations, but it is for some simple
but important models that I will now examine.





Next: Flat water-bottom
Up: Alvarez: Multiples in image
Previous: Introduction
Stanford Exploration Project
11/1/2005


![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , consists of four
segments, such that the total travel-time for the multiple is given by
, consists of four
segments, such that the total travel-time for the multiple is given by

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , at any given depth the image space coordinates
of the migrated multiple are given by:
, at any given depth the image space coordinates
of the migrated multiple are given by:
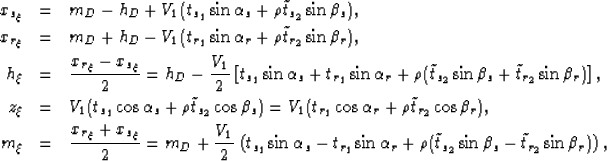
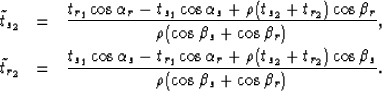
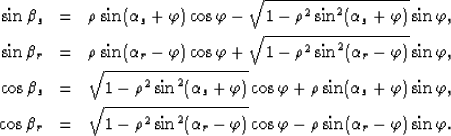

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The half-aperture angle is given by
.
The half-aperture angle is given by