




Next: About this document ...
Up: Alvarez: Multiples in image
Previous: From dip to no
From Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we can immediately compute the takeoff
angle of the diffracted receiver ray as
we can immediately compute the takeoff
angle of the diffracted receiver ray as
| ![\begin{displaymath}
\alpha_r=\tan^{-1}\left[\frac{h_D+m_D-X_{diff}}{Z_{diff}}\right].\end{displaymath}](img84.gif) |
(78) |
mul_sktch13
Figure 26 Sketch showing the
geometry of the zero surface half-offset diffracted multiple from a
dipping water-bottom.
|
| 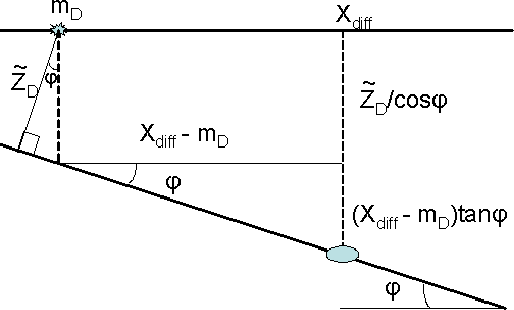 |

In this equation the depth of the diffractor is not known, but it can be
calculated from the geometry of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) :
:
|  |
(79) |
As we did for the diffracted multiple from the flat water-bottom, we can
use the traveltime of the multiple at the zero surface-offset trace to compute
 , except that this time the computation is much more involved.
Figure
, except that this time the computation is much more involved.
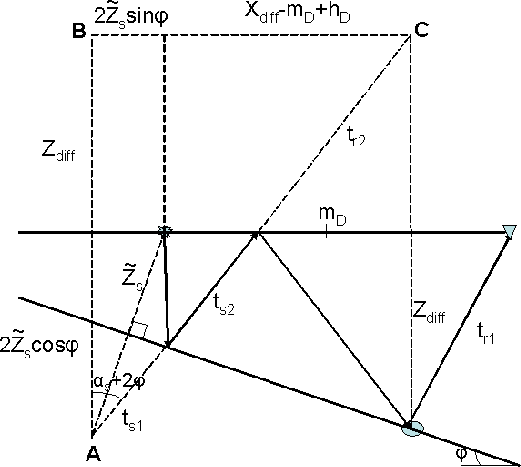
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the basic geometry. From triangle ABC we
have
shows the basic geometry. From triangle ABC we
have
| ![\begin{displaymath}[V_1(t_m(0)-t_{r_1}(0))]
^2=(2\tilde{Z}_D\cos\varphi+Z_{diff})^2+(2\tilde{Z}_D\sin\varphi+(X_{diff}-m_D))^2,\end{displaymath}](img113.gif) |
(80) |
were tr1 is the traveltime of the diffracted segment that, according
to triangle DEF in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is given by
is given by
|
[V1tr1(0)]2=Zdiff2+(Xdiff-mD)2.
|
(81) |

Replacing equations 79 and 81 into equation 80
gives a quartic equation for  which can be solved numerically.
Once
which can be solved numerically.
Once 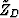 is known, we can easily compute Zdiff with
equation 79 and therefore
is known, we can easily compute Zdiff with
equation 79 and therefore 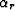 with equation 78
in terms of the known quantities hD, mD, Xdiff and tm(0).
with equation 78
in terms of the known quantities hD, mD, Xdiff and tm(0).
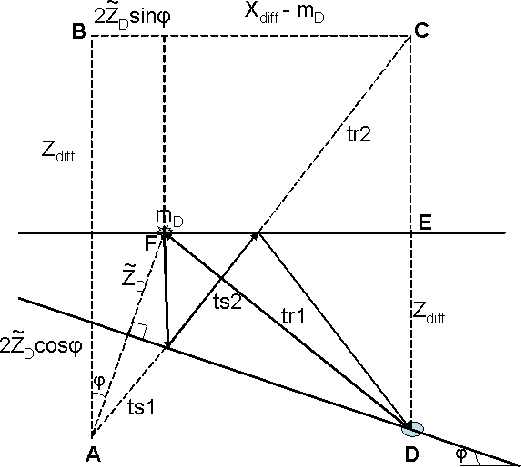
mul_sktch15
Figure 28 Sketch to compute
the takeoff angle of the source ray from a diffracted multiple.
|
|  |

In order to compute 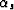 , we apply the law of sines to triangle ABC
in Figure
, we apply the law of sines to triangle ABC
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to get
to get
| 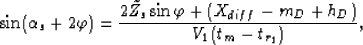 |
(82) |
where 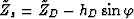 and V1tr1 is the
length of the diffracted receiver ray and is given by
and V1tr1 is the
length of the diffracted receiver ray and is given by
| 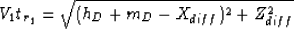 |
(83) |
Therefore, plugging equation 83 into equation 82 we get
equation 50:
| ![\begin{displaymath}
\alpha_s=\sin^{-1}\left[\frac{2\tilde{Z}_D\sin\varphi+(h_D+X...
...V_1t_m-\sqrt{(h_D+m_D-X_{diff})^2+Z_{diff}^2}}\right]-2\varphi.\end{displaymath}](img87.gif) |
(84) |





Next: About this document ...
Up: Alvarez: Multiples in image
Previous: From dip to no
Stanford Exploration Project
11/1/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we can immediately compute the takeoff
angle of the diffracted receiver ray as
we can immediately compute the takeoff
angle of the diffracted receiver ray as

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) :
:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the basic geometry. From triangle ABC we
have
shows the basic geometry. From triangle ABC we
have
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is given by
is given by
![]() which can be solved numerically.
Once
which can be solved numerically.
Once ![]() is known, we can easily compute Zdiff with
equation 79 and therefore
is known, we can easily compute Zdiff with
equation 79 and therefore ![]() with equation 78
in terms of the known quantities hD, mD, Xdiff and tm(0).
with equation 78
in terms of the known quantities hD, mD, Xdiff and tm(0).

![]() , we apply the law of sines to triangle ABC
in Figure
, we apply the law of sines to triangle ABC
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to get
to get
![\begin{displaymath}
\alpha_s=\sin^{-1}\left[\frac{2\tilde{Z}_D\sin\varphi+(h_D+X...
...V_1t_m-\sqrt{(h_D+m_D-X_{diff})^2+Z_{diff}^2}}\right]-2\varphi.\end{displaymath}](img87.gif)