




Next: Examples
Up: CANONICAL FUNCTIONS AND THE
Previous: Estimation schemes based on
In order to have a more precise model for comparison purposes,
and to get a better feeling for just how much difference it makes
whether we model the microstructure very accurately or not, we will now
consider a model material called a ``random polycrystal of laminates.''
Suppose we construct a random polycrystal by packing small bits of
a laminate material (i.e., a composite layered along a
symmetry axis) into a large container in a way so that the
axis of symmetry of the grains appears randomly over all possible
orientations and also such that no misfit of surfaces (and therefore
porosity) is left in the resulting composite.
If the ratio of laminate grain size to overall
composite is small enough so the usual implicit assumption of
scale separation applies to the composite -- but not so small that
we are violating the continuum hypothesis -- then we have an example
of a random polycrystal of laminates. See schematic in Figure 1.
The analytical advantage of this model is that the layers can be
composed of the two elastic constituents in the composites discussed
here previously. Furthermore, the elastic behavior of the laminate
material itself can be predicted using well-known exact methods
(Backus, 1962).
We will not dwell on these details here, but just
make use of the results to be found in many publications
(Berryman, 2004b). The only results needed in the
following are the Reuss and Voigt averages for the grains, which are
1/KR = 2s11 + 2s12 + 4s13 + s33 for Reuss in terms of
compliances, or
| 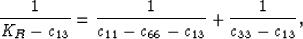 |
(19) |
in terms of stiffness, and
| ![\begin{displaymath}
K_V = \left[2(c_{11}+c_{12}) +4c_{13}+c_{33}\right]/9
\end{displaymath}](img75.gif) |
(20) |
for the Voigt average of bulk modulus. Similarly, the Voigt
average for shear of the stiffness matrix may be written as
| 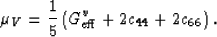 |
(21) |
This expression can be taken as the definition of 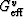 .Eq.(21) implies that
.Eq.(21) implies that 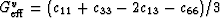 . In fact,
. In fact, 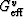 is the energy
per unit volume in a grain when a pure uniaxial shear strain of
unit magnitude is applied to the grain along its axis of symmetry
(Berryman, 2004a,b). Then, the Reuss average for shear is
is the energy
per unit volume in a grain when a pure uniaxial shear strain of
unit magnitude is applied to the grain along its axis of symmetry
(Berryman, 2004a,b). Then, the Reuss average for shear is
| ![\begin{displaymath}
\mu_R = \left[\frac{1}{5}\left(\frac{1}{G_{\rm eff}^r} + \frac{2}{c_{44}}
+ \frac{2}{c_{66}}\right)\right]^{-1},
\end{displaymath}](img79.gif) |
(22) |
which is also a rigorous lower bound on the overall shear modulus of
the polycrystal (Hill, 1952). Each laminated grain thus has hexagonal
symmetry, so the product formulas
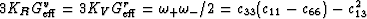 are valid (Berryman, 2004a).
The symbols
are valid (Berryman, 2004a).
The symbols 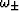 stand for the quasi-compressional and
quasi-uniaxial shear eigenvalues for all the grains.
stand for the quasi-compressional and
quasi-uniaxial shear eigenvalues for all the grains.
Once this notation has been established, then it is straightforward to
express the Peselnick-Meister bounds (Peselnick and Meister, 1965)
for hexagonal symmetry as
| 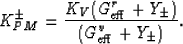 |
(23) |
for effective bulk modulus K* of the polycrystal,
where
| 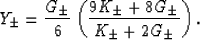 |
(24) |
The precise values of the parameters 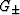 and
and 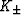 (being shear
and bulk moduli of the HS isotropic comparison material) were given
algorithmically by Watt and Peselnick (1980.) Similarly,
(being shear
and bulk moduli of the HS isotropic comparison material) were given
algorithmically by Watt and Peselnick (1980.) Similarly,
| ![\begin{displaymath}
\frac{1}{\mu_{PM}^\pm + Y_\pm} =
\frac{1}{5}\big[\frac{1-A_...
..._\pm} + \frac{2}{c_{44}+Y_\pm} + \frac{2}{c_{66}+Y_\pm}\big],
\end{displaymath}](img86.gif) |
(25) |
for the effective shear modulus 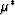 of the polycrystal.
The meaning of
of the polycrystal.
The meaning of 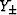 is the same in (23) and
(25). Here
is the same in (23) and
(25). Here 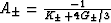 ,
,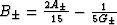 ,and
,and 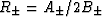 . These bounds are of Hashin-Shtrikman type,
but were first obtained for hexagonal symmetry by Peselnick and
Meister (1965) with some corrections supplied later by
Watt and Peselnick (1980).
. These bounds are of Hashin-Shtrikman type,
but were first obtained for hexagonal symmetry by Peselnick and
Meister (1965) with some corrections supplied later by
Watt and Peselnick (1980).
Since we now have analytical forms for the bounds in
(23)-(25), it seems it should be
possible to arrive at self-consistent formulas (estimates related to
the bounds) by making substitutions 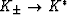 and
and 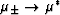 ,as well as
,as well as 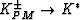 and
and 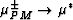 .This procedure can be followed without difficulty for the bulk modulus
bounds in (23). However, for the shear modulus
estimator, we need to take into account a step in the derivation
of (25) that restricted its applicability to a certain
curve in the (
.This procedure can be followed without difficulty for the bulk modulus
bounds in (23). However, for the shear modulus
estimator, we need to take into account a step in the derivation
of (25) that restricted its applicability to a certain
curve in the (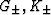 )-plane. Since the self-consistent
estimate will not normally lie on this curve, we need to back up in
the analysis presented by Watt and Peselnick (1980) and take into account
a correction term that vanishes along the curve in question but not in
general. When we do this, and also make use of the self-consistent
formula for the bulk modulus K*, which is
)-plane. Since the self-consistent
estimate will not normally lie on this curve, we need to back up in
the analysis presented by Watt and Peselnick (1980) and take into account
a correction term that vanishes along the curve in question but not in
general. When we do this, and also make use of the self-consistent
formula for the bulk modulus K*, which is
| 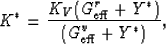 |
(26) |
we find that the self-consistent estimator for the shear modulus
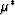 is
is
| ![\begin{displaymath}
\frac{1}{\mu^* + Y^*} =
\frac{1}{5}\left[\frac{1-A^*(K_V-K^...
... + Y^*} + \frac{2}{c_{44}+Y^*} + \frac{2}{c_{66}+Y^*}\right].
\end{displaymath}](img97.gif) |
(27) |
The transform variable for these two formulas is just
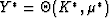 , with
, with 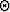 defined as in (4).
defined as in (4).
From the derivation, it is expected that these self-consistent
estimates based on the polycrystal bounds will always lie between the
bounds. In fact, this feature is observed in all the results from
calculations done using these formulas. It can also be shown that
the self-consistent estimator obtained this way is the same as that
found by Willis (1981) using different arguments. Furthermore, the
results are also in agreement with the self-consistent formulas
of Olson and Avellaneda (1992)
for polycrystals composed of spherical grains when their
results for orthorhombic symmetry are specialized to hexagonal symmetry.





Next: Examples
Up: CANONICAL FUNCTIONS AND THE
Previous: Estimation schemes based on
Stanford Exploration Project
5/3/2005
![\begin{displaymath}
\mu_R = \left[\frac{1}{5}\left(\frac{1}{G_{\rm eff}^r} + \frac{2}{c_{44}}
+ \frac{2}{c_{66}}\right)\right]^{-1},
\end{displaymath}](img79.gif)
![]() and
and ![]() ,as well as
,as well as ![]() and
and ![]() .This procedure can be followed without difficulty for the bulk modulus
bounds in (23). However, for the shear modulus
estimator, we need to take into account a step in the derivation
of (25) that restricted its applicability to a certain
curve in the (
.This procedure can be followed without difficulty for the bulk modulus
bounds in (23). However, for the shear modulus
estimator, we need to take into account a step in the derivation
of (25) that restricted its applicability to a certain
curve in the (![]() )-plane. Since the self-consistent
estimate will not normally lie on this curve, we need to back up in
the analysis presented by Watt and Peselnick (1980) and take into account
a correction term that vanishes along the curve in question but not in
general. When we do this, and also make use of the self-consistent
formula for the bulk modulus K*, which is
)-plane. Since the self-consistent
estimate will not normally lie on this curve, we need to back up in
the analysis presented by Watt and Peselnick (1980) and take into account
a correction term that vanishes along the curve in question but not in
general. When we do this, and also make use of the self-consistent
formula for the bulk modulus K*, which is