Examples

We will now provide some examples of elastic constant bounds and estimates.

 

GSCblkmd
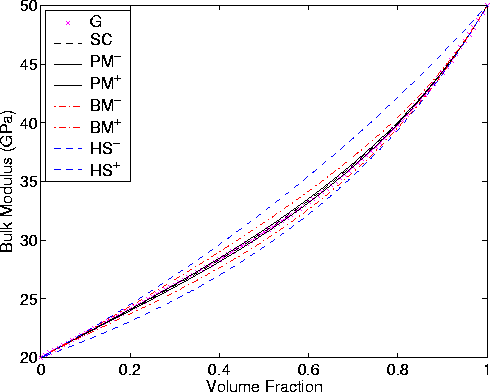
Figure 2 Comparison of (a) the (uncorrelated) bounds of Hashin and Shtrikman (HS$^\pm$), (b) the microstructure-based bounds (assuming disk inclusions) of Beran and Molyneaux (BM$^\pm$) for bulk modulus, and (c) the random polycrystal bounds of Peselnick and Meister (PM$^\pm$)assuming that the composite is an aggregate of randomly oriented laminated (hexagonal symmetry) grains. A self-consistent (SC) estimate based on the Peselnick-Meister bounds lies between the PM$^\pm$ bounds for both bulk and shear moduli. A new estimator (G) is based on the BM and MPT bounds and uses a geometric mean approximation in order to incorporate information contained in the microstructure constants $\zeta_i$ and $\eta_i$.

 

GSCshrmd
Figure 3 As in Figure 1, but the Milton and Phan-Thien (MPT$^\pm$) bounds are used instead for shear modulus.

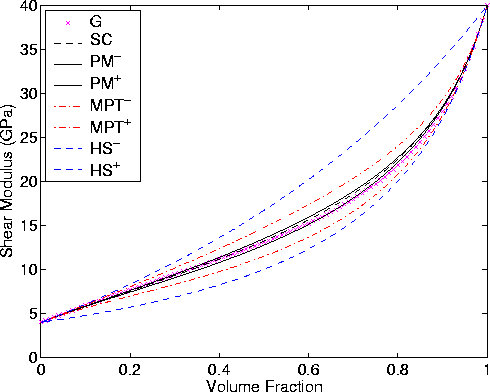Figures 2 and 3 provide some examples of elastic constant bounds and estimates for a system having two constituents with K₁ = 20, K₂ = 50, $\mu_1 = 4$, $\mu_2 = 40$, all constants measured in GPa.

The Hashin-Shtrikman (uncorrelated) bounds (HS$^\pm$) are the outer most bounds for both bulk and shear modulus. The Beran-Molyneux (BM$^\pm$) bounds for bulk modulus and the Milton-Phan-Thien (MPT$^\pm$) bounds for shear modulus -- in both cases the shapes of the inclusions are assumed to be disk-like -- are the next bounds as we move inward. Then the Peselnick-Meister (PM$^\pm$) bounds for polycrystals of hexagonal grains are applied to grains laminated so that their volume fractions of type-1 and type-2 are always the same as that of the overall composite being considered here. These PM$^\pm$ bounds lie strictly inside the BM$^\pm$ and MPT$^\pm$ bounds. Then the inner most curve is the SC curve generated as described here by using the analytical forms of the PM$^\pm$ bounds to construct self-consistent estimates for the random polycrystal of laminates model. This SC curve is always inside the PM$^\pm$ bounds and therefore inside all the bounds considered here. Finally, we have the geometric mean estimates G, based on the improved bounds of BM$^\pm$ and MPT$^\pm$.These estimates always lie between these two bounds, but not always inside the PM$^\pm$ bounds. This result shows that the BM and MPT bounds are allowing for a wider range of microstructures than are the PM bounds, which is entirely reasonable under the circumstances. The main practical observation however is that the PM$^\pm$, SC, and G curves (both bounds and estimates) are in fact all very close to each other (differing by less than 2% maximum for this high contrast example). This fact suggests that any or all of these curves could be used when designing new composites having preassigned elastic properties, or for analysis of seismic wave data for interpretation purposes. The errors in these predictions would likely be close to the experimental errors in the construction of such composites and therefore negligible for many, though perhaps not all, practical purposes.