Next: Elasticity for random polycrystals
Up: CANONICAL FUNCTIONS AND THE
Previous: Rigorous bounds
One very famous approximation scheme for elastic composites
is due to Hill (1952). The idea is to take the known Voigt and Reuss averages of the
elastic system stiffnesses or compliances,
and then make direct use of this information by
computing either the arithmetic or geometric mean of these two limiting
values. These formulas have been found to be very effective for fitting
real data in a wide variety of circumstances
(Simmons and Wang, 1971; Thomsen, 1972; Watt and Peselnick 1980).
Clearly the same basic idea can be applied to any pairs of bounds
for scalars, such as the Hashin-Shtrikman bounds;
or, for complex constants, a similar idea based on
finding the center-of-mass of a bounded region in the complex plane
could be pursued (but to date apparently has not been). The advantage
of such approaches is that they can provide the user
with just one estimate per choice of volume fraction,
while at the same time requiring no additional information
over that contained in the bounds themselves.
Hill's concept clearly works just as well, and possibly somewhat
better, if we apply it instead -- whenever we have an analytical function
at our disposal as we do here in the canonical functions
-- to the transform variables 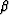 and
and
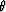 rather than to the moduli K and
rather than to the moduli K and 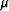 directly. So one set
of estimates we might test in our examples takes the form
directly. So one set
of estimates we might test in our examples takes the form
| 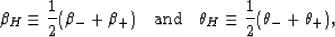 |
(10) |
where the bounds on 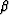 and
and 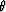 were already given in TABLE 1, and the averages are just the arithmetic means. The
subscript H is intended to reference Hill's contribution to this
idea.
were already given in TABLE 1, and the averages are just the arithmetic means. The
subscript H is intended to reference Hill's contribution to this
idea.
Another rather different approach (although still expected to give
quite similar results) is to examine the forms of the 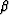 and
and
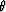 transform variables in order to determine if some other
estimate that lies between the bounds might suggest itself.
One useful tool we can introduce here is the weighted geometric
mean. For example,
if we define
transform variables in order to determine if some other
estimate that lies between the bounds might suggest itself.
One useful tool we can introduce here is the weighted geometric
mean. For example,
if we define
| 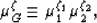 |
(11) |
it is well-known (Hardy et al., 1952) that this is a geometric mean
and it always lies between (or on) the corresponding mean
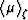 and harmonic mean
and harmonic mean
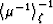 :
:
| 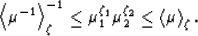 |
(12) |
So 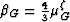 is one natural choice we could make for
the bulk modulus transform parameter estimate. This approach has one
clear advantage over the usual self-consistent estimates in that
the microstructural information can easily be incorporated this way,
whereas the means of doing so for self-consistent methods usually
involves more complicated calculations via scattering theory
(Gubernatis and Krumhansl, 1975; Berryman, 1980).
This approach also provides a
formula, rather than an implicit equation requiring an iteration
procedure for its solution, thus eliminating another common criticism
of implicit estimators.
is one natural choice we could make for
the bulk modulus transform parameter estimate. This approach has one
clear advantage over the usual self-consistent estimates in that
the microstructural information can easily be incorporated this way,
whereas the means of doing so for self-consistent methods usually
involves more complicated calculations via scattering theory
(Gubernatis and Krumhansl, 1975; Berryman, 1980).
This approach also provides a
formula, rather than an implicit equation requiring an iteration
procedure for its solution, thus eliminating another common criticism
of implicit estimators.
Similar results are not as easy to find for the shear modulus bounds.
The reason is that there are either two or three averages that come
into play for shear, always including
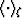 and
and 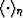 ,while the formulas (5) and (6) also depend on the usual
volume averages
,while the formulas (5) and (6) also depend on the usual
volume averages 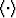 . Since it is known that the
McCoy-Silnutzer bounds are never tighter than those of
Milton and Phan-Thien (1982), we will consider only the Milton and Phan-Thien bounds from here on,
since they have only two types of averages present.
. Since it is known that the
McCoy-Silnutzer bounds are never tighter than those of
Milton and Phan-Thien (1982), we will consider only the Milton and Phan-Thien bounds from here on,
since they have only two types of averages present.
In general 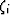 and
and 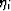 differ. But in some cases (spheres
and disks, for example) they are the same. Furthermore, it is easy to
show that for any modulus M, we have the result (relevant in
particular to needles) that
differ. But in some cases (spheres
and disks, for example) they are the same. Furthermore, it is easy to
show that for any modulus M, we have the result (relevant in
particular to needles) that
| ![\begin{displaymath}
\begin{array}
{r}
\left<M\right\gt _\eta - \left<M\right\gt ...
...ght\gt\right] \
= \frac{1}{12}(v_1-v_2)(M_1-M_2).
\end{array} \end{displaymath}](img53.gif) |
(13) |
Thus, the differences always vanish for 50-50 concentrations, and
furthermore the factor of 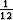 reduces the difference
further by an order of magnitude. If we make the approximation that
reduces the difference
further by an order of magnitude. If we make the approximation that
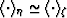 , this
is often a quite reasonable compromise. When this is so, we can
then choose to make the further approximations that
, this
is often a quite reasonable compromise. When this is so, we can
then choose to make the further approximations that
| 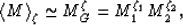 |
(14) |
and also that
| 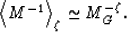 |
(15) |
Substituting these approximations into the Milton and Phan-Thien
bounds (7) and (8), we find that both
transform parameters for the upper and lower bounds are
replaced by the same effective transform parameter:
| 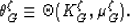 |
(16) |
This result provides a unique estimate that will always lie
between these bounds.
A somewhat better (i.e., more balanced)
approximation is achieved for 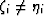 by defining
by defining 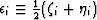 . Then, all
occurrences
of
. Then, all
occurrences
of 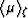 ,
, 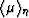 ,
,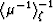 , and
, and
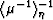 are replaced by
are replaced by 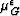 .
The errors introduced now through differences
.
The errors introduced now through differences 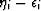 are
half those in (13). But new errors are introduced
through the differences
are
half those in (13). But new errors are introduced
through the differences 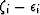 . The resulting geometric
approximation turns out to be
. The resulting geometric
approximation turns out to be
| 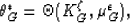 |
(17) |
which still reduces to (16) whenever 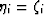 .Also note that, if
.Also note that, if 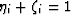 , then
, then
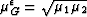 .
.
[Note:
If 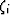 is known but
is known but 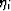 is not known (either experimentally
or theoretically), Berryman and Milton (1988) discuss how
to use knowledge of
is not known (either experimentally
or theoretically), Berryman and Milton (1988) discuss how
to use knowledge of 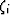 to constrain estimates of
to constrain estimates of 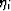 .However, we will not pursue this option here.]
.However, we will not pursue this option here.]
To maintain internal consistency of the approximation, we can choose
to set
| 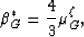 |
(18) |
or we could choose instead to use 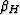 from
(10). However,
we do not expect that these choices will differ by very much for the
bulk modulus estimates.
from
(10). However,
we do not expect that these choices will differ by very much for the
bulk modulus estimates.
laminated_poly_l12
Figure 1 Schematic illustrating the model
of random polycrystals of laminates. Grains are assumed to fit
tightly so there is no misfit porosity.
But the shapes of the grains are not necessarily the same, and the
symmetry axes of the grains (three examples are shown here) are
randomly oriented so the overall polycrystal is equiaxed
(statistically isotropic).






Next: Elasticity for random polycrystals
Up: CANONICAL FUNCTIONS AND THE
Previous: Rigorous bounds
Stanford Exploration Project
5/3/2005
![]() and
and
![]() rather than to the moduli K and
rather than to the moduli K and ![]() directly. So one set
of estimates we might test in our examples takes the form
directly. So one set
of estimates we might test in our examples takes the form
![]() and
and
![]() transform variables in order to determine if some other
estimate that lies between the bounds might suggest itself.
One useful tool we can introduce here is the weighted geometric
mean. For example,
if we define
transform variables in order to determine if some other
estimate that lies between the bounds might suggest itself.
One useful tool we can introduce here is the weighted geometric
mean. For example,
if we define
![]() and
and ![]() ,while the formulas (5) and (6) also depend on the usual
volume averages
,while the formulas (5) and (6) also depend on the usual
volume averages ![]() . Since it is known that the
McCoy-Silnutzer bounds are never tighter than those of
Milton and Phan-Thien (1982), we will consider only the Milton and Phan-Thien bounds from here on,
since they have only two types of averages present.
. Since it is known that the
McCoy-Silnutzer bounds are never tighter than those of
Milton and Phan-Thien (1982), we will consider only the Milton and Phan-Thien bounds from here on,
since they have only two types of averages present.
![]() and
and ![]() differ. But in some cases (spheres
and disks, for example) they are the same. Furthermore, it is easy to
show that for any modulus M, we have the result (relevant in
particular to needles) that
differ. But in some cases (spheres
and disks, for example) they are the same. Furthermore, it is easy to
show that for any modulus M, we have the result (relevant in
particular to needles) that
![]() by defining
by defining ![]() . Then, all
occurrences
of
. Then, all
occurrences
of ![]() ,
, ![]() ,
,![]() , and
, and
![]() are replaced by
are replaced by ![]() .
The errors introduced now through differences
.
The errors introduced now through differences ![]() are
half those in (13). But new errors are introduced
through the differences
are
half those in (13). But new errors are introduced
through the differences ![]() . The resulting geometric
approximation turns out to be
. The resulting geometric
approximation turns out to be
![]() is known but
is known but ![]() is not known (either experimentally
or theoretically), Berryman and Milton (1988) discuss how
to use knowledge of
is not known (either experimentally
or theoretically), Berryman and Milton (1988) discuss how
to use knowledge of ![]() to constrain estimates of
to constrain estimates of ![]() .However, we will not pursue this option here.]
.However, we will not pursue this option here.]