




Next: Combined Data and Model
Up: methodology
Previous: Consistency of the Data
Visual inspection of Figure 3 motivates the two forms of
regularization utilized in this paper. Find any first-order multiple on the section marked
``NMO for Primaries''. Notice that the corresponding event on the first- and second-order
pseudo-primary panels, originally second- and third-order multiples, respectively, all have
a different moveout. In fact, the only events which are kinematically consistent across all
offsets are the flattened primary and pseudo-primaries. The other events, all crosstalk, are
inconsistent between panels. Therefore, the first regularization
operator seeks to penalize the difference between the 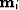 , at fixed
, at fixed  . To account
for the dissimilarity of the AVO of primaries and multiples, this difference is taken at
different offsets, as defined in equation (4). Written in the form of a model
residual vector, this difference is:
. To account
for the dissimilarity of the AVO of primaries and multiples, this difference is taken at
different offsets, as defined in equation (4). Written in the form of a model
residual vector, this difference is:
| ![\begin{displaymath}
\bold r_m^{[1]}(\tau,x,i) = m_i(\tau,h_p) - m_{i+1}(\tau,x).\end{displaymath}](img20.gif) |
(8) |
The third index in equation (9), i, ranges from 0 to np-1, where
np is the highest order multiple modeled in the inversion [see equation (6)].
The second form of regularization used in this paper is the more obvious of the two:
a difference operator along offset. This difference exploits the fact that all
non-primaries are not flat after NMO. Again, we can write this difference in the form
of a model residual vector:
| ![\begin{displaymath}
\bold r_m^{[2]}(\tau,x,i) = m_i(\tau,x) - m_i(\tau,x+\Delta x).\end{displaymath}](img21.gif) |
(9) |
The second regularization is applied to all the 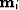 . A similar approach is used
by Prucha et al. (2001) to regularize prestack depth migration in the angle
domain.
. A similar approach is used
by Prucha et al. (2001) to regularize prestack depth migration in the angle
domain.





Next: Combined Data and Model
Up: methodology
Previous: Consistency of the Data
Stanford Exploration Project
6/10/2002