Consistency of the Data and the Crosstalk Problem

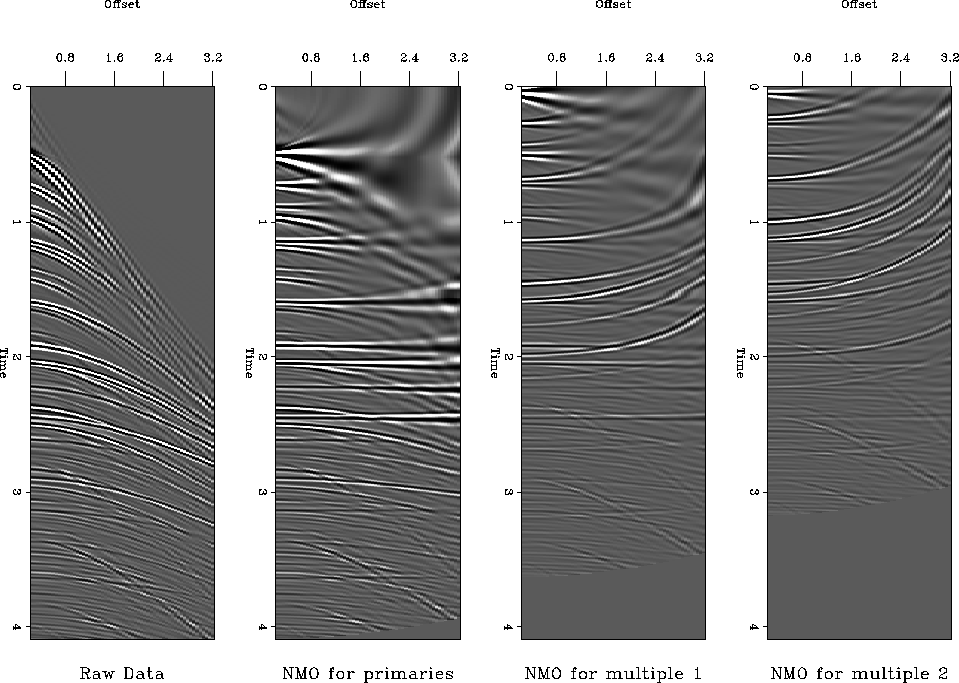
Figure 3 shows the result of applying the adjoint of equation (6) to a synthetic CMP gather which was constructed by an elastic modeling scheme. Imagine for a moment that the CMP gather consists only of primaries and first- and second-order water-bottom multiples. The ``NMO for Primaries'' panel would contain flattened primaries (signal) and downward-curving first- and second-order multiples (noise). Likewise, the ``NMO for multiple 1'' and ``NMO for multiple 2'' panels contain flattened signal and curving noise. Why do I call these components ``signal'' and ``noise''? If each of the three panels contained all signal and no noise, then we could 1) perfectly reconstruct the data from the model by applying equation (6), and 2) be in the enviable position of having a perfect estimate of the primaries.

 

schem.hask
Figure 3 From left to right: Raw synthetic CMP gather; Conventional NMO applied to data; NMO for first-order water-bottom multiple; NMO for second-order water-bottom multiples.

Unfortunately, the curved events - so-called ``crosstalk'' - in all three model panels spoil this idealized situation Claerbout (1992). Because the crosstalk events map back to actual events in the data, they are difficult to suppress in a least-squares minimization of the data residual [equation (7)]. Nemeth et al. (1999) shows that crosstalk relates directly to non-invertibility of the Hessian (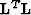$\bold L^T \bold L$), and that data-space or model-space regularization may partially overcome the difficulty. In the following section, I introduce a novel form of model-space regularization which promotes discrimination of signal from crosstalk.