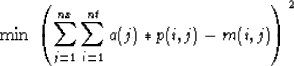Next: Least-squares imaging of multiples
Up: methodology
Previous: NMO for Multiple Reflections
Even after application of the water-bottom reflection coefficient, the AVO response of the
pseudo-primary section created by equation (1) does not match that of the
corresponding NMO-corrected primary section. Refer to Figure 2 and note that
for constant-AVO water-bottom reflection (and a free surface reflection coefficient of
-1), the amplitude of the water-bottom multiple at
offset hp+hm is simply the amplitude of the primary at offset hp, scaled by the
negative water-bottom reflection coefficient. Still, the question remains: what are hm
and hp? For the case of constant velocity, we can use trigonometry to derive hm
and hp as a function of the zero offset traveltimes of the primary reflection and
water bottom ( and
and 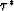 , respectively), and the source-receiver offset x.
In constant velocity, the multiple and primary legs of the raypath are similar triangles:
, respectively), and the source-receiver offset x.
In constant velocity, the multiple and primary legs of the raypath are similar triangles:
| 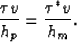 |
(3) |
Also, for a first-order water-bottom multiple,
hp + hm = x.
These two independent equations can be solved and simplified to give expressions for
hp and hm:
| 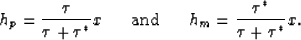 |
(4) |
I omit the general form of the expression for orders of multiple higher than one, although
it is straightforward to derive.
avo
Figure 2 Assuming a constant AVO water-bottom reflection
and constant velocity, we can write the AVO of water-bottom multiples with offset hp+hm
as a function of the AVO of the primary recorded at a shorter offset, hp.
|
| 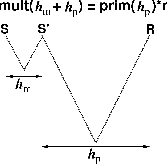 |

To obtain an estimate of the water-bottom reflection coefficient, I solve a simple least squares
problem to estimate a function of location, 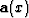 , which when applied to a small window of
dimension
, which when applied to a small window of
dimension 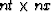 around the NMO-corrected water-bottom reflection,
around the NMO-corrected water-bottom reflection, 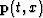 , optimally resembles the NMO-corrected
[equation (1)] first-order water-bottom multiple reflection,
, optimally resembles the NMO-corrected
[equation (1)] first-order water-bottom multiple reflection, 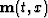 . To achieve
this,
. To achieve
this, 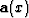 is perturbed to minimize the following quadratic functional.
is perturbed to minimize the following quadratic functional.
| 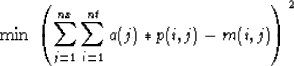 |
(5) |
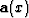 may not be reliable at far offsets, due to either NMO stretch or non-hyperbolicity,
so in practice, an estimate of the single best-fitting water-bottom reflection coefficient
is made using the
may not be reliable at far offsets, due to either NMO stretch or non-hyperbolicity,
so in practice, an estimate of the single best-fitting water-bottom reflection coefficient
is made using the 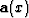 from ``useful'' offsets only.
from ``useful'' offsets only.





Next: Least-squares imaging of multiples
Up: methodology
Previous: NMO for Multiple Reflections
Stanford Exploration Project
6/10/2002
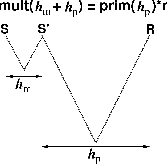
![]() , which when applied to a small window of
dimension
, which when applied to a small window of
dimension ![]() around the NMO-corrected water-bottom reflection,
around the NMO-corrected water-bottom reflection, ![]() , optimally resembles the NMO-corrected
[equation (1)] first-order water-bottom multiple reflection,
, optimally resembles the NMO-corrected
[equation (1)] first-order water-bottom multiple reflection, ![]() . To achieve
this,
. To achieve
this, ![]() is perturbed to minimize the following quadratic functional.
is perturbed to minimize the following quadratic functional.