




Next: Interpolation theory
Up: Three-dimensional seismic data regularization
Previous: Acknowledgments
Forward interpolation
As I will illustrate in later chapters, the crucial part of data
regularization problems is in the choice and implementation of the
regularization operator 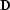 or the corresponding
preconditioning operator
or the corresponding
preconditioning operator 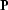 . The choice of the forward
modeling operator
. The choice of the forward
modeling operator 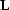 is less critical. In this chapter, I
discuss the nature of forward interpolation, which has been one of the
traditional subjects in computational mathematics. Wolberg (1990)
presents a detailed review of different conventional approaches. I
discuss a simple mathematical theory of interpolation from a regular
grid and derive the main formulas from a very general idea of function
bases.
is less critical. In this chapter, I
discuss the nature of forward interpolation, which has been one of the
traditional subjects in computational mathematics. Wolberg (1990)
presents a detailed review of different conventional approaches. I
discuss a simple mathematical theory of interpolation from a regular
grid and derive the main formulas from a very general idea of function
bases.
Forward interpolation plays only a supplementary role in this
dissertation, but it has many primary applications, such as trace
resampling, NMO, Kirchhoff and Stolt migrations, log-stretch, and
radial transform, in seismic data processing and imaging. Two simple
examples appear at the end of this chapter.





Next: Interpolation theory
Up: Three-dimensional seismic data regularization
Previous: Acknowledgments
Stanford Exploration Project
12/28/2000