| |
(45) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to be
) to be
| |
(46) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and its
spectrum are shown in Figure
) and its
spectrum are shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The spectrum is
identically equal to 1 in the Nyquist frequency band.
. The spectrum is
identically equal to 1 in the Nyquist frequency band.
 |
Function (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is well-known as the Shannon sinc
interpolant. According to the sampling theorem
Kotel'nikov (1933); Shannon (1949), it provides an optimal interpolation for
band-limited signals. A known problem prohibiting its practical
implementation is the slow decay with (x - n), which results in a
far too expensive computation. This problem is solved in practice with
heuristic tapering Hale (1980), such as triangle tapering
Harlan (1982), or more sophisticated taper windows
Wolberg (1990). One popular choice is the Kaiser window Kaiser and Shafer (1980),
which has the form
) is well-known as the Shannon sinc
interpolant. According to the sampling theorem
Kotel'nikov (1933); Shannon (1949), it provides an optimal interpolation for
band-limited signals. A known problem prohibiting its practical
implementation is the slow decay with (x - n), which results in a
far too expensive computation. This problem is solved in practice with
heuristic tapering Hale (1980), such as triangle tapering
Harlan (1982), or more sophisticated taper windows
Wolberg (1990). One popular choice is the Kaiser window Kaiser and Shafer (1980),
which has the form
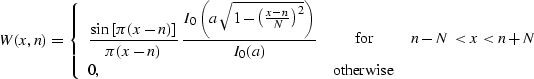 |
(47) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) has the
adjustable parameter a, which controls the behavior of its
spectrum. I have found empirically the value of a=4 to provide
a spectrum that deviates from 1 by no more than 1% in a relatively
wide band.
) has the
adjustable parameter a, which controls the behavior of its
spectrum. I have found empirically the value of a=4 to provide
a spectrum that deviates from 1 by no more than 1% in a relatively
wide band.
While the function W from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) automatically
satisfies properties (
) automatically
satisfies properties (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), where both
x and n range from
), where both
x and n range from ![]() to
to ![]() , its tapered version may
require additional normalization.
, its tapered version may
require additional normalization.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the interpolation error of the
8-point Kaiser-tapered sinc interpolant with that of cubic convolution
on the example from Figure
compares the interpolation error of the
8-point Kaiser-tapered sinc interpolant with that of cubic convolution
on the example from Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The accuracy improvement
is clearly visible.
. The accuracy improvement
is clearly visible.
|
cubkai
Figure 8 Interpolation error of the cubic-convolution interpolant (dashed line) compared to that of an 8-point windowed sinc interpolant (solid line). |  |
The differences among the described forward interpolation methods are
also clearly visible from the discrete spectra of the corresponding
interpolants. The left plots in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show discrete interpolation responses: the
function W(x,n) for a fixed value of x=0.7. The right plots
compare the corresponding discrete spectra. Clearly, the spectrum gets
flatter and wider as the accuracy of the method increases.
show discrete interpolation responses: the
function W(x,n) for a fixed value of x=0.7. The right plots
compare the corresponding discrete spectra. Clearly, the spectrum gets
flatter and wider as the accuracy of the method increases.
|
speclincub
Figure 9 Discrete interpolation responses of linear and cubic convolution interpolants (left) and their discrete spectra (right) for x=0.7. | 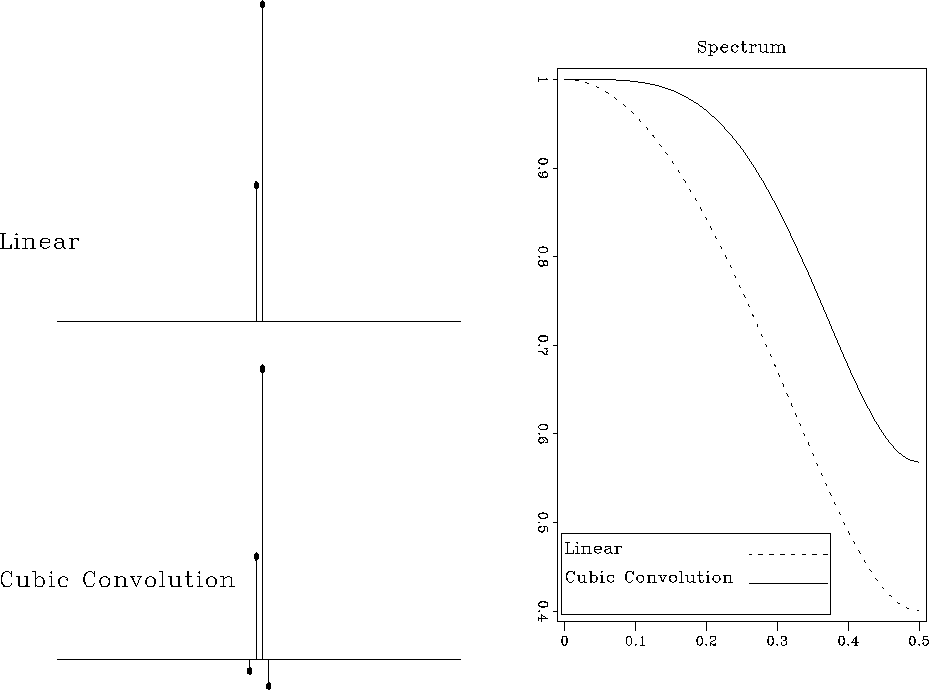 |
|
speccubkai
Figure 10 Discrete interpolation responses of cubic convolution and 8-point windowed sinc interpolants (left) and their discrete spectra (right) for x=0.7. | 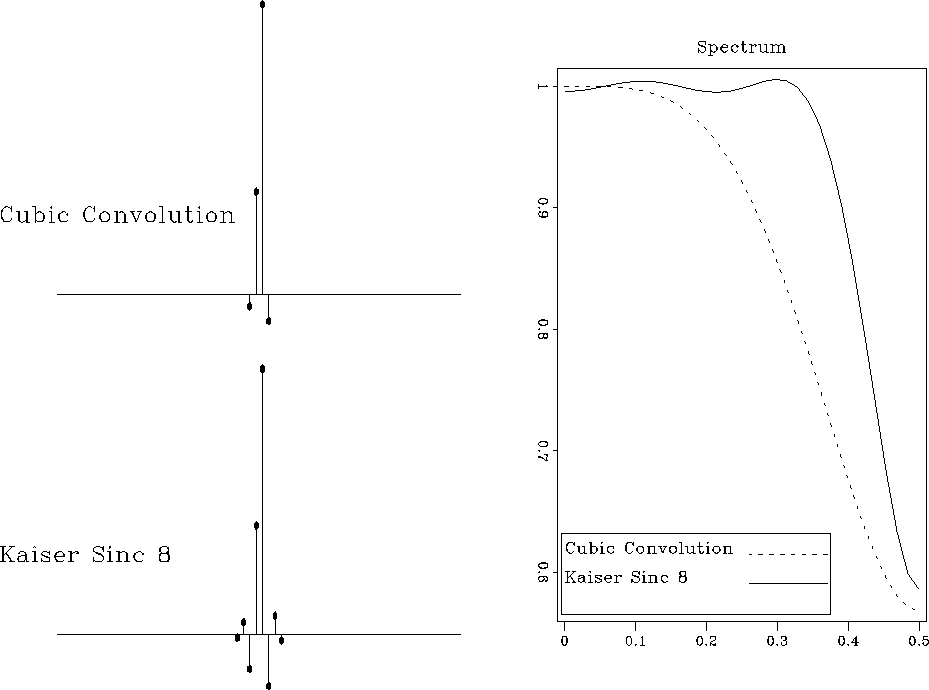 |