




Next: Solution
Up: Forward interpolation
Previous: Interpolation theory
A particular form of the solution (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) arises from
assuming the existence of a basis function set
) arises from
assuming the existence of a basis function set 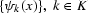 , such that the function f (x) can be represented by a linear
combination of the basis functions in the set, as follows:
, such that the function f (x) can be represented by a linear
combination of the basis functions in the set, as follows:
|  |
(33) |
We can find the linear coefficients ck by multiplying both
sides of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) by one of the basis functions
(e.g.
) by one of the basis functions
(e.g. 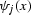 ). Inverting the equality
). Inverting the equality
| 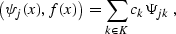 |
(34) |
where the parentheses denote the dot product, and
| 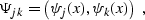 |
(35) |
leads to the following explicit expression for the coefficients
ck:
| 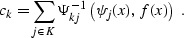 |
(36) |
Here 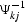 refers to the kj component of the matrix,
which is the inverse of
refers to the kj component of the matrix,
which is the inverse of 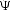 . The matrix
. The matrix 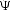 is invertible as
long as the basis set of functions is linearly independent. In the
special case of an orthonormal basis,
is invertible as
long as the basis set of functions is linearly independent. In the
special case of an orthonormal basis, 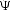 reduces to the identity
matrix:
reduces to the identity
matrix:
| 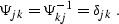 |
(37) |
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is a least-squares estimate of the coefficients
ck: one can alternatively derive it by minimizing the least-squares
norm of the difference between f(x) and the linear
decomposition (
) is a least-squares estimate of the coefficients
ck: one can alternatively derive it by minimizing the least-squares
norm of the difference between f(x) and the linear
decomposition (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). For a given set of basis functions,
equation (
). For a given set of basis functions,
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) approximates the function f(x) in formula
(
) approximates the function f(x) in formula
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the least-squares sense.
) in the least-squares sense.





Next: Solution
Up: Forward interpolation
Previous: Interpolation theory
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) arises from
assuming the existence of a basis function set
) arises from
assuming the existence of a basis function set ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) by one of the basis functions
(e.g.
) by one of the basis functions
(e.g. ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is a least-squares estimate of the coefficients
ck: one can alternatively derive it by minimizing the least-squares
norm of the difference between f(x) and the linear
decomposition (
) is a least-squares estimate of the coefficients
ck: one can alternatively derive it by minimizing the least-squares
norm of the difference between f(x) and the linear
decomposition (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). For a given set of basis functions,
equation (
). For a given set of basis functions,
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) approximates the function f(x) in formula
(
) approximates the function f(x) in formula
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the least-squares sense.
) in the least-squares sense.