Beyond B-splines

It is not too difficult to construct a convolutional basis with more accurate interpolation properties than those of B-splines, for example by sacrificing the function smoothness. The following piece-wise cubic function has a lower smoothness than $\beta^3(x)$ in equation () but slightly better interpolation behavior:  

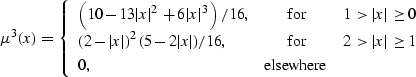$$\mu^3(x) = \left\{\begin{array} {lcr} \displaystyle \left(1... ...vert x\vert \geq 1 \\ 0, & \mbox{elsewhere} &\end{array}\right.$$ (72)

Figures and compare the test interpolation errors and discrete responses of methods based on the B-spline function $\beta^3(x)$ and the lower smoothness function $\mu^3(x)$. The latter method has a slight but visible performance advantage and a slightly wider discrete spectrum.

 

splmom4 Figure 25 Interpolation error of the third-order B-spline interpolant (dashed line) compared to that of the lower smoothness spline interpolant (solid line).

 

specsplmom4 Figure 26 Discrete interpolation responses of third-order B-spline and lower smoothness spline interpolants (left) and their discrete spectra (right) for x=0.7. A slight but visible difference in the interpolation responses accounts for a small improvement in accuracy.

Blu et al. (1998) have developed a general approach for constructing non-smooth piece-wise functions with optimal interpolation properties. However, the gain in accuracy is often negligible in practice. In the rest of the dissertation, I use the classic and better tested B-spline method.