Synthetic examples

In this section I apply the Kirchhoff, phase-shift, and finite-difference wave-equation datuming operators to synthetic data in order to compare them and to demonstrate some basic characteristics of the datuming process. To gain the full benefit of wave-equation datuming, data should generally be datumed prestack; however, I examine the zero-offset case here because it is a first step in gaining intuition into how wave-equation datuming transforms the data and also because it is easy to visualize what the zero-offset synthetics should look like.

The subsurface model for the synthetic data consists of an anticline, a syncline, and two point diffractors in a constant velocity media. The medium velocity is 2 km/s. Topography is modeled as a 200 m high cosine shaped mountain (Figure ). The result of zero-offset Kirchhoff modeling is shown in Figure a. The effect of the topography is the creation of a low frequency undulation which completely distorts the synthetic data.

 

submodel Figure 6 Synthetic subsurface model and topography. Topography and subsurface structure used to generate the zero-offset synthetic data. The two point diffractors are depicted by astrecies above and below the anticline/syncline structure.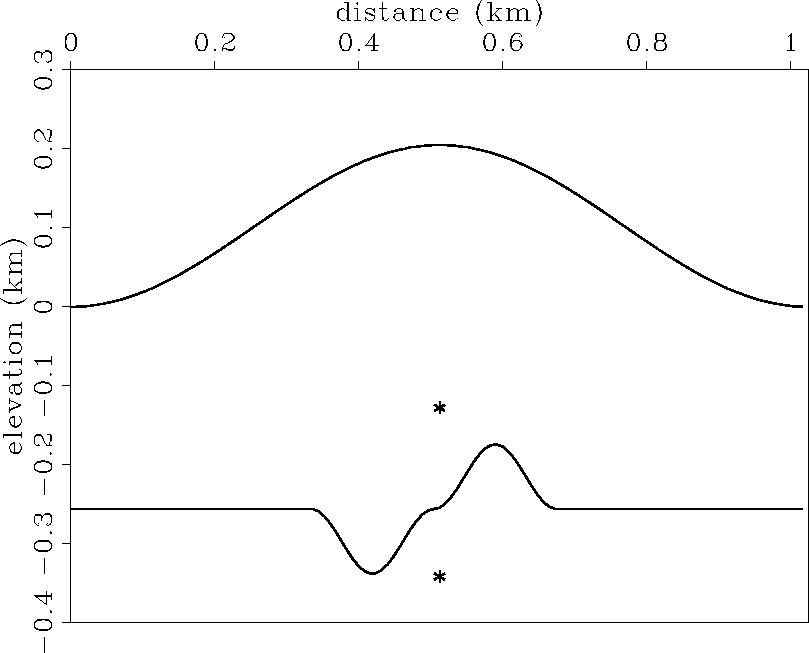