![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), where the Wi operators
represent the Kirchhoff extrapolation operator between small
depth intervals
), where the Wi operators
represent the Kirchhoff extrapolation operator between small
depth intervals
Kirchhoff datuming can be applied recursively, as in the case of
finite-difference and phase-shift datuming. This recursive formulation is
embodied in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), where the Wi operators
represent the Kirchhoff extrapolation operator between small
depth intervals
), where the Wi operators
represent the Kirchhoff extrapolation operator between small
depth intervals ![]() . Since the depth intervals are small,
the time delay
. Since the depth intervals are small,
the time delay ![]() is short and the computation is definitely in the
near field, so it is important to retain the near-field term.
Because the extrapolation distance is short, fewer traces can be
taken into the integral operator. However, the short extrapolation
distance makes the Kirchhoff summation trajectory very steep, necessitating
a high degree of operator anti-aliasing for data right at the apex of
the summation trajectories. When the depth step is small, the
Kirchhoff operator approaches the limit of becoming an explicit
finite-difference extrapolator, and all of the difficulties of
designing such an operator begin to manifest themselves.
is short and the computation is definitely in the
near field, so it is important to retain the near-field term.
Because the extrapolation distance is short, fewer traces can be
taken into the integral operator. However, the short extrapolation
distance makes the Kirchhoff summation trajectory very steep, necessitating
a high degree of operator anti-aliasing for data right at the apex of
the summation trajectories. When the depth step is small, the
Kirchhoff operator approaches the limit of becoming an explicit
finite-difference extrapolator, and all of the difficulties of
designing such an operator begin to manifest themselves.
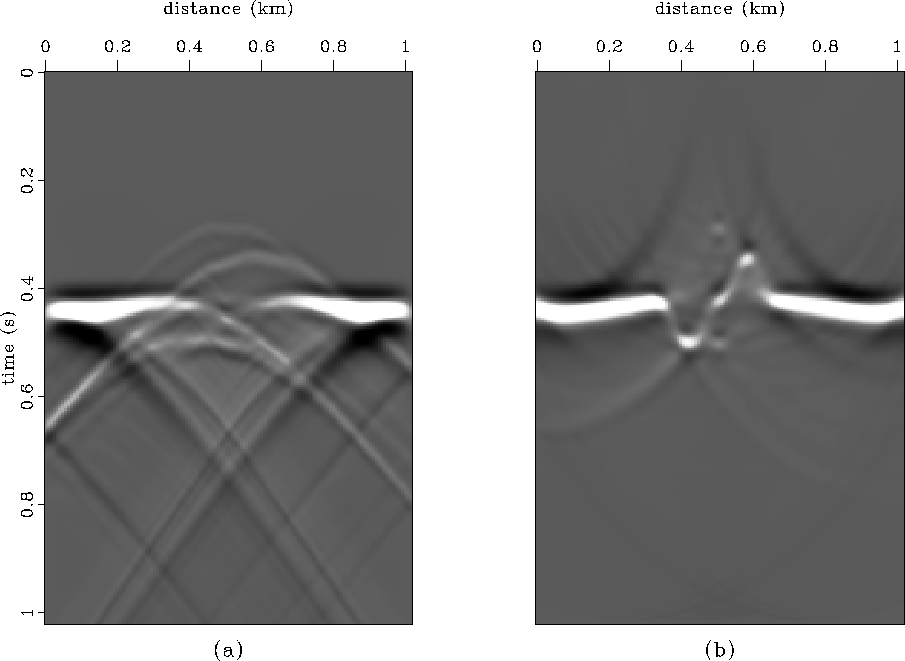
The result of upward continuing the synthetic data with the
recursive Kirchhoff datuming algorithm is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Ten traces were used for every application of the Kirchhoff extrapolator
and the same number of depth levels (21) were used as in the phase-shift
and finite-difference results. The datuming and migration results
are much more low frequency because of the high degree of anti-aliasing
required, and the steep dip resolution has decreased because of the
limited width of the extrapolator.
The migrated image in Figure
.
Ten traces were used for every application of the Kirchhoff extrapolator
and the same number of depth levels (21) were used as in the phase-shift
and finite-difference results. The datuming and migration results
are much more low frequency because of the high degree of anti-aliasing
required, and the steep dip resolution has decreased because of the
limited width of the extrapolator.
The migrated image in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b
looks more like the image after finite-difference datuming
(Figure
b
looks more like the image after finite-difference datuming
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c) than after
Kirchhoff datuming (Figure
c) than after
Kirchhoff datuming (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b).
b).
The importance of keeping the near-field term is illustrated in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . When the far-field approximation is made, the
recursive extrapolation is overcome by strong artifacts.
. When the far-field approximation is made, the
recursive extrapolation is overcome by strong artifacts.
 |
 |
The recursive Kirchhoff extrapolator results in poorer results than any of the aformentioned methods and is very inefficient computationally. I have presented it merely to demonstrate how the datuming methods can be linked. In practice there are much more efficient methods of recursive explicit extrapolation.