Next: Near-field vs. far-field Kirchhoff
Up: Synthetic examples
Previous: Upward continuation
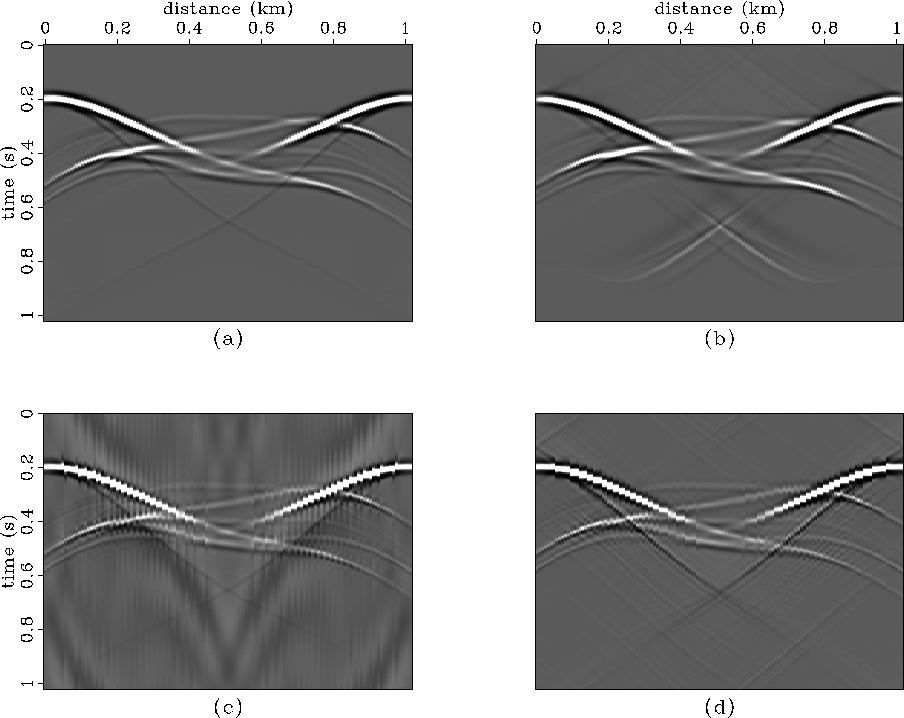
In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the upward continued synthetics of Figure
, the upward continued synthetics of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) have been downward continued back to the original recording surface using
the adjoint datuming operators. The Kirchhoff method has most faithfully
reproduced the original synthetic. Both the finite-difference and the
phase-shift result have a pronounced stair-step effect along the events.
This does not occur after upward continuation, but after downward
continuation, the discretisation of the topography has introduced
an error. This error can be reduced at the cost of a finer
grid step size in
have been downward continued back to the original recording surface using
the adjoint datuming operators. The Kirchhoff method has most faithfully
reproduced the original synthetic. Both the finite-difference and the
phase-shift result have a pronounced stair-step effect along the events.
This does not occur after upward continuation, but after downward
continuation, the discretisation of the topography has introduced
an error. This error can be reduced at the cost of a finer
grid step size in  . Aside from the stair-step effect, both the
finite-difference and phase-shift results reasonably restore the
original kinematics, although the finite-difference result exhibits
more artifacts.
. Aside from the stair-step effect, both the
finite-difference and phase-shift results reasonably restore the
original kinematics, although the finite-difference result exhibits
more artifacts.
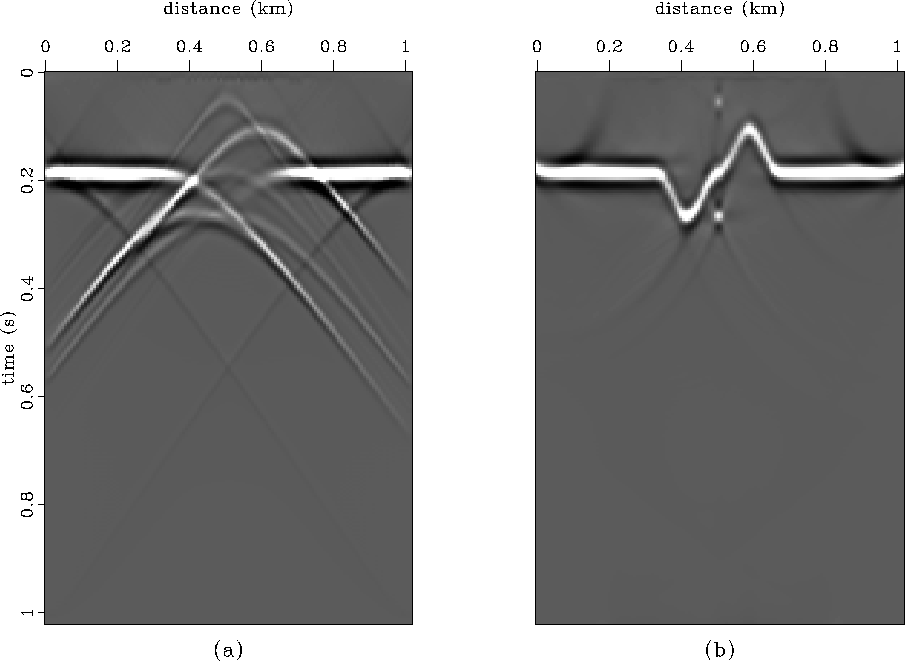
The result of downward continuing the original synthetic (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a)
from the topography to a flat datum below the topography
with the Kirchhoff algorithm is displayed in Figure
a)
from the topography to a flat datum below the topography
with the Kirchhoff algorithm is displayed in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Downward continuing the data in constant (or depth-variable) velocity
does not require trace padding because all dip components are
propagated downward and inward and the steep dips do not
propagate off the computational grid. Therefore, the flanks
of the syncline/anticline
structure are well imaged without requiring any trace padding.
.
Downward continuing the data in constant (or depth-variable) velocity
does not require trace padding because all dip components are
propagated downward and inward and the steep dips do not
propagate off the computational grid. Therefore, the flanks
of the syncline/anticline
structure are well imaged without requiring any trace padding.
datdn
Figure 10 (a) Synthetic data, and downward continuation
of the upward continued synthetics from Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with (b) Kirchhoff,
(c) finite-difference, and (d) phase-shift methods.
with (b) Kirchhoff,
(c) finite-difference, and (d) phase-shift methods.




 datdnmig
datdnmig
Figure 11 Downward continuation and migration of downward continued synthetic
with the Kirchhoff algorithm.










Next: Near-field vs. far-field Kirchhoff
Up: Synthetic examples
Previous: Upward continuation
Stanford Exploration Project
2/12/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the upward continued synthetics of Figure
, the upward continued synthetics of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) have been downward continued back to the original recording surface using
the adjoint datuming operators. The Kirchhoff method has most faithfully
reproduced the original synthetic. Both the finite-difference and the
phase-shift result have a pronounced stair-step effect along the events.
This does not occur after upward continuation, but after downward
continuation, the discretisation of the topography has introduced
an error. This error can be reduced at the cost of a finer
grid step size in
have been downward continued back to the original recording surface using
the adjoint datuming operators. The Kirchhoff method has most faithfully
reproduced the original synthetic. Both the finite-difference and the
phase-shift result have a pronounced stair-step effect along the events.
This does not occur after upward continuation, but after downward
continuation, the discretisation of the topography has introduced
an error. This error can be reduced at the cost of a finer
grid step size in