 |
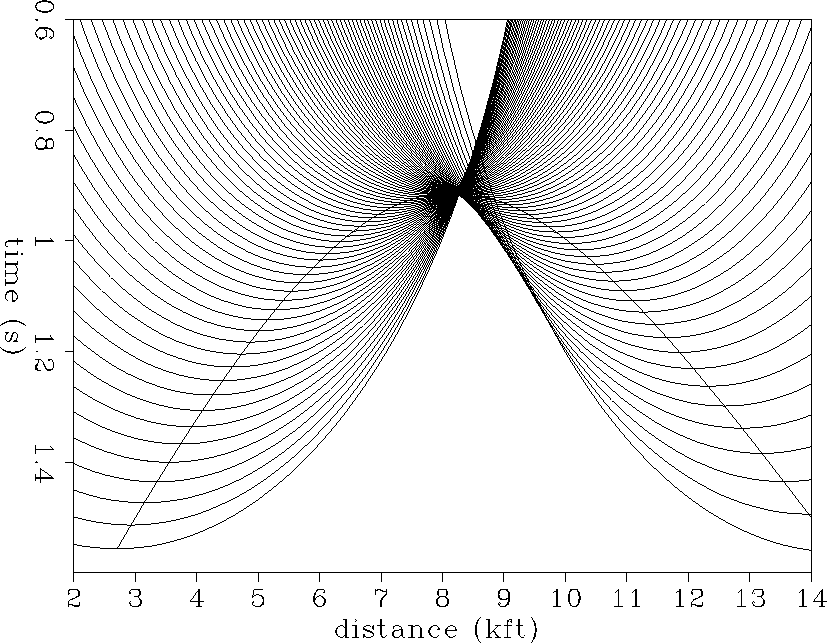
Figure 3 Time migration semi-circles are superimposed on the true-diffraction curve for the dipping-layer model. The points where the semi-circles add constructively form the migrated image.
Time migration may be thought of as hyperbola summation or semi-circle superposition Schneider (1978). In order to illustrate the kinematics of time migration when there are lateral velocity variations, we first superimpose time migration semi-circles along the diffraction curve of Figure 2. This geometrical construction is shown in Figure 3, where the radius of each circle is determined by the RMS velocity that would be derived from a well drilled straight down to the diffractor from the surface at the diffractor location. This value is 8.846 kft/sec and is what we call as the well RMS velocity. This is the migration velocity used throughout this paper. The points where the semi-circles add constructively form the time-migrated image of the point diffractor. Figure 4 is an enlarged view showing the semi-circle superposition near the apex of the true-diffraction curve. The envelope of semi-circles is displaced to the right of the true diffractor position at 8 kft and forms a distinctive cusp shape that opens to the right. This shape is what we call the ``plume.'' The plume shows that the various dip components of a point diffractor end up at different positions on the time-migrated image. Thus the plume clearly shows that mis-focusing occurs when time migration is applied to a medium with lateral velocity variations.
 |
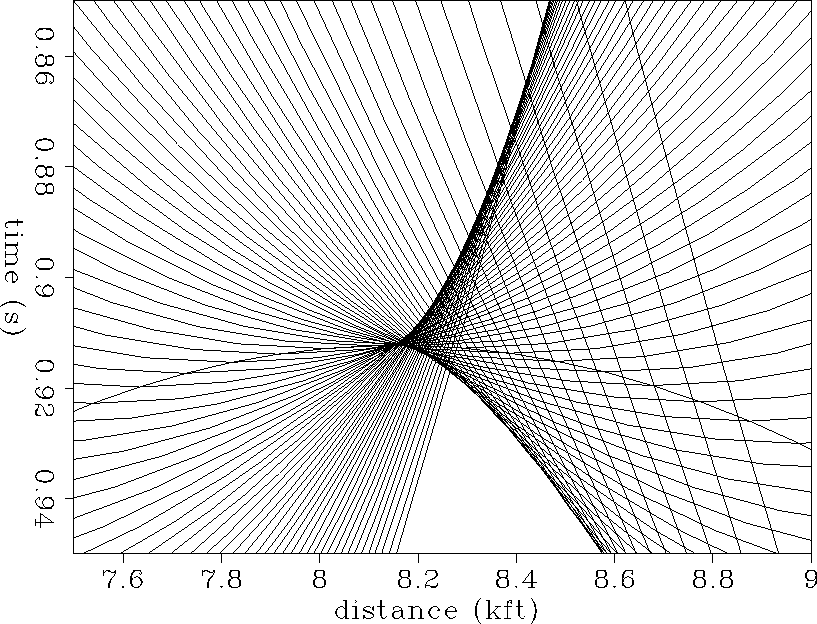 |
The plume shape can be qualitatively explained by examining the kinematics of time migration. For the left side of the true-diffraction curve the migration velocity is too fast, so that limb of the curve is overmigrated. For the right side of the true-diffraction curve the migration velocity is too slow, so that limb of the curve is undermigrated.