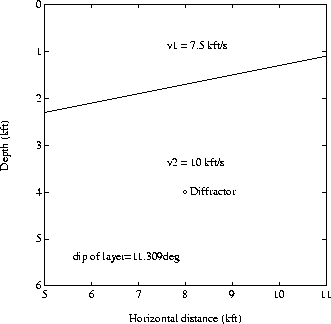
 |
Figure 1 Dipping-layer model. The change in velocity across the dipping layer causes an implicit velocity gradient which depends on the dip of the layer.
The model used in this paper is displayed in Figure 1. An implicit velocity gradient is caused by the dipping layer since the velocity changes across it. We begin our study by analyzing the response of a point diffractor positioned below the layer. The parameters of the model were chosen to match the synthetic data example given by Black and Brzostowski 1993. The point diffractor is positioned at a depth of 4 kft at a horizontal position of 8 kft.
The true-diffraction curve for this model is the zero-offset response to a point diffractor. Ray-tracing with equations (A-4) and (A-5) of the Appendix shows that this curve is asymmetric (Figure 2). The arrival times are later where the low velocity wedge is thicker and earlier where the wedge is thinner. The apex of the curve is offset to the right of the diffractor position.
 |
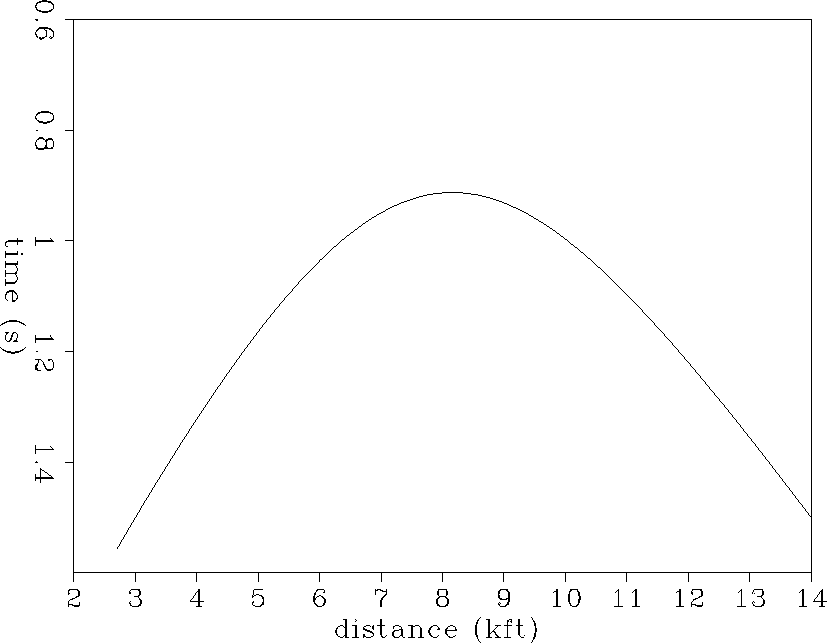 |