




Next: About this document ...
Up: Black et. al.: Time
Previous: ACKNOWLEDGEMENTS
- Bevc, D., 1992, Kirchhoff wave-equation datuming with irregular acquisition topography: SEP-75, 137-156.
-
- Black, J. L., and Brzostowski, M. A., 1993, Systematics of time-migration errors: Accepted for publication in Geophysics.
-
- Claerbout, J. F., 1992, Anti aliasing: SEP-73, 371-390.
-
- Hatton, L., Larner, K. L., and Gibson, B. S., 1981, Migration of seismic data from inhomogeneous media: Geophysics, 46, no. 5, 751-767.
-
- Hubral, P., 1977, Time migration - some ray theoretical aspects: Geophys. Prosp., 25, no. 4, 738-745.
-
- Larner, K. L., Hatton, L., Gibson, B. S., and Hsu, I. C., 1981, Depth migration of imaged time sections: Geophysics, 46, no. 5, 734-750.
-
- Schneider, W. A., 1978, Integral formulation for migration in two-dimensions and three-dimensions: Geophysics, 43, no. 1, 49-76.
-
- Yilmaz, O., 1987, Seismic data processing: Soc. Expl. Geophys.
-
APPENDIX A
In this Appendix, we derive the analytical formulae used to obtain the
ray-tracing results for the dipping layer model and the tangent construction
migration.
The first step is to model the asymmetric true-diffraction curve.
This is done by applying
Snell's law at the point R where the normal ray crosses the interface
in Figure 10.
Snell's law at R is given by
| 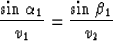 |
(9) |
where 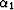 and
and 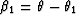 are the angles
of incidence at the interface. The vertical
distances (a1,a2) are expressed in terms of the
vertical distances (d1,d2) at the migrated
position. From the geometry of Figure 10 we get
are the angles
of incidence at the interface. The vertical
distances (a1,a2) are expressed in terms of the
vertical distances (d1,d2) at the migrated
position. From the geometry of Figure 10 we get
| 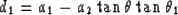 |
(10) |
| 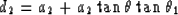 |
(11) |
We now wish to derive the x-displacement along the normal
ray. From Figure 10 we see that this is the sum of two terms:
| 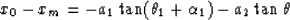 |
(12) |
the travel time along the normal ray is given by
| 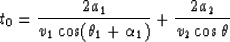 |
(13) |
The apparent time dip D at the earth's surface is given by
| 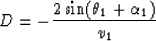 |
(14) |
Equations (A-4) and (A-5) define the true-diffraction curve
(Figure 2).
Common-tangent migration is performed by matching the time dip D
(equation (A-6)) with the dip of the time migration curve
and moving the point to the apex of the time migration curve.
Carrying out this procedure as discussed in the main text results in
Figure 5.





Next: About this document ...
Up: Black et. al.: Time
Previous: ACKNOWLEDGEMENTS
Stanford Exploration Project
11/17/1997