Hyperbola Summation

The semi-circle superposition method allows us to visualize how the plume is built up from constructive interference. It does not, however, offer a convenient way to numerically compute the actual shape of the plume. A more effective way to compute the time-migration response to a point diffractor is by summing along hyperbolas Schneider (1978). The analytical technique for summing along hyperbolas is called the ``common- tangent'' construction. It relies on the fact that the main contribution to the sum comes from the place where a time-migration hyperbola is tangent to the true-diffraction curve of Figure 2. The event at the tangency point is positioned by time migration to the apex of the time-migration hyperbola.

The time migration hyperbola is given by:  

$${t_0^2} = {t_k^2} + 4{[{x_0 - x_k \over V(x_m ,t_m)}]}^2$$ (1)

Matching the slope of the hyperbola given by equation(1) with the time dip D of the event leads to the following formulas for the position of the time migrated point (x_k,t_k):  

$$x_k = x_0 - {[{V(x_m,t_m)D \over 2}] [{V(x_m,t_m)t_0 \over 2}]}$$ (2)

 

$$t_k = t_0 \sqrt {1 - {[{V(x_m,t_m)D \over 2}]}^2}$$ (3)

where

$$D = {\partial t_0 \over {\partial {x_0}}}$$

is the apparent time dip of the event to be migrated and V(x_m,t_m) is the RMS well velocity at the diffractor location.

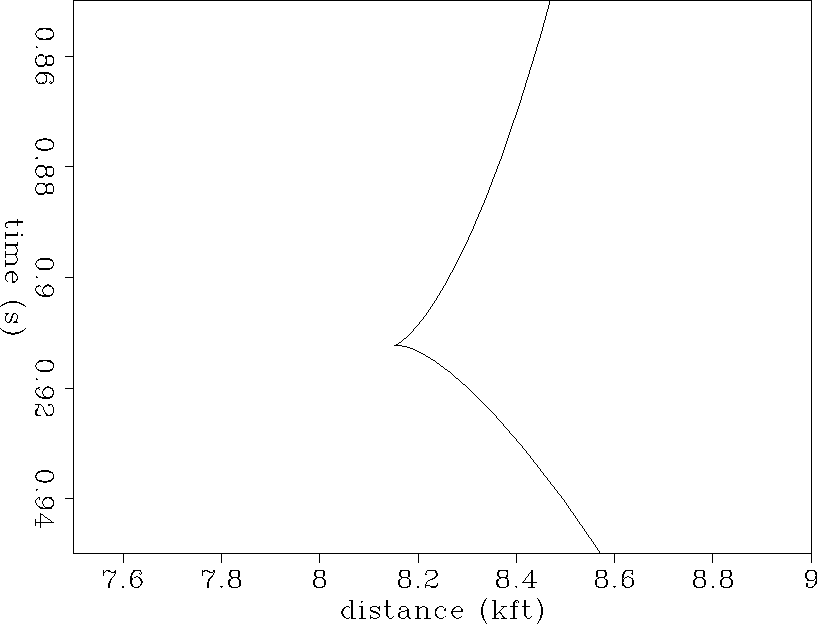
This procedure is then carried out for each point along the true-diffraction curve to yield the complete response of time migration to a point diffractor. Details of the algebra of this computation are given in the Appendix and the results are shown in Figure 5. In generating this figure we have again used the vertical RMS well velocity that was used in Figure 3. Note that the plume envelope in Figure 4 matches the curve in Figure 5 exactly. Thus the two ways of geometrically constructing the time-migration response to lateral velocity variation are consistent with each other.

 

vwell
Figure 5 Plume derived by hyperbola summation with the common-tangent construction. This curve corresponds to the envelope of semicircles in Figure 4 exactly.