Kirchoff's type representations of the DKO for the homogeneous medium prompts the general form of an integral KO:
| |
(99) |
where ![]() - negative weight function,
- negative weight function, ![]() - propagation time
from
- propagation time
from ![]() to
to ![]() with accordance with a given
eiconal equation
with accordance with a given
eiconal equation
| |
(100) |
Without any lack of generality we can put n=0. We propose that
![]()
![]()
| |
(101) |
It is well known that
![]()
It is easy to show that when point ![]() is placed behind the front
is placed behind the front ![]() (where
(where ![]() is the correspondent solution of equation (100) with
condition
is the correspondent solution of equation (100) with
condition ![]() ), then argument of
), then argument of ![]() -function at
-function at
![]() is always positive:
is always positive:
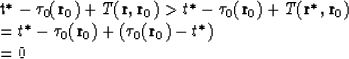 |
||
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). It means that in this case,
). It means that in this case,