




Next: 10: EXTREMAL VELOCITIES
Up: 9: INTEGRAL OPERATORS OF
Previous: Amplitude equivalence
If w=w1w2 and 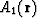 is a discontinuity amplitude of the field
is a discontinuity amplitude of the field
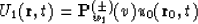
(where 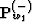 is the KO with the kernel w1)
then the discontinuity of the field
is the KO with the kernel w1)
then the discontinuity of the field
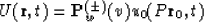
has the amplitude
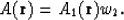
In particular, it means that if
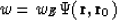
and AE is the amplitude of the field
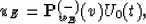
then for field 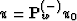 has discontinuity amplitude:
has discontinuity amplitude:
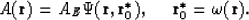
Here, dependence 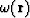 means that
means that 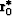 belongs to the same ray of eiconal
belongs to the same ray of eiconal
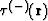 .
.





Next: 10: EXTREMAL VELOCITIES
Up: 9: INTEGRAL OPERATORS OF
Previous: Amplitude equivalence
Stanford Exploration Project
1/13/1998
![]()
![]()
![]()
![]()
![]()
![]()