![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Then
).
Then
We shall propose that points ![]() ,
, ![]() and
and ![]() lie on the same
ray
lie on the same
ray ![]() of eiconal
of eiconal ![]() (Figure
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Then
).
Then
![]()
![]()
![]()
![]()
After substituting into the equation (101) at ![]() and
and ![]() and performing
rather rigorous transformations, we obtain that
and performing
rather rigorous transformations, we obtain that
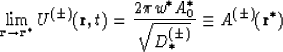
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) different locations of fronts
different locations of fronts It is easy to derive from the pictures that
![]()
![]()