




Next: Amplitude equivalence
Up: 9: INTEGRAL OPERATORS OF
Previous: Formulas for amplitudes (3D
If we use the same type of considerations as in the 3D case, we receive
![\begin{displaymath}
U^{(-)}({\bf r},t)={1 \over \sqrt{\pi d^{(-)}}}{wA_0H[\tau({\bf r})-t] \over
\sqrt{\tau^{(-)}({\bf r})-t}}+\psi({\bf r})\end{displaymath}](img557.gif)
where 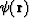 is a smooth function,
is a smooth function,
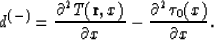
Let us expand the class of discontinuities
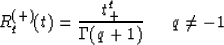
with arbitrary (noninteger) q, and
R(-)q(t) = R(+)q(-t).
We must also expand the notion of q-equivalence (which was introduced in the Chapter 1) to a noninteger q: 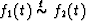 if
if 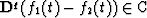 .The operator of noninteger differentiation
.The operator of noninteger differentiation 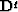 was considered above for q=1/2 (see Chapter 8). For arbitrary q it can be defined by spectra response
was considered above for q=1/2 (see Chapter 8). For arbitrary q it can be defined by spectra response
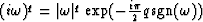 .
.
It can be shown that
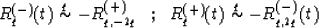
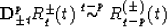
It is easy to see that
![\begin{displaymath}
U^{(-)}({\bf r},t) \sim {wA_0 \over \sqrt{d^{(-)}}} R^{(-)}_{-{1 \over2}}
[t-\tau^{(-)}({\bf r})]\end{displaymath}](img567.gif)
and
![\begin{displaymath}
u({\bf r},t) \sim {wA_0 \over \sqrt{d^{(-)}}} R^{(-)}_{q+{1 \over2}}
[t-\tau^{(-)}({\bf r})]\end{displaymath}](img568.gif)
(it is proposed that d(-)>0).
If d(-)<0, then
![\begin{displaymath}
U^{(-)} \sim {wA_0 \over \sqrt{\vert d^{(-)}\vert}} R^{(+)}_{-{1 \over2}}
[t-\tau^{(-)}({\bf r})]\end{displaymath}](img569.gif)
and general formula
![\begin{displaymath}
U^{(-)} \sim \kappa {wA_0 \over \sqrt{\vert d^{(-)}\vert}}
R^{(-)}_{-{1 \over2},{1- \kappa \over 2}}
[t-\tau^{(-)}]\end{displaymath}](img570.gif)
where 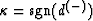 .
.
Let d(-)=0. We introduce the order of touching of curves 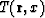 and
and 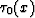 :the order = p if
:the order = p if
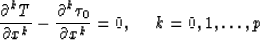
and
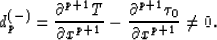
If the order p is even, then
![\begin{displaymath}
u^{(\pm)} \sim A_p[R^{(+)}_{q+{1 \over p+1}}(t-\tau^{(-)})+R^{(-)}_{q+{1 \over p+1}}
(t-\tau^{(-)})]\end{displaymath}](img576.gif)
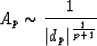
If the order is uneven
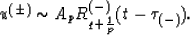
The point  is a special one if, for given
is a special one if, for given  and
and 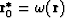 ,
,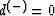 .Each special point of the order p=2 is the point on caustics.
.Each special point of the order p=2 is the point on caustics.





Next: Amplitude equivalence
Up: 9: INTEGRAL OPERATORS OF
Previous: Formulas for amplitudes (3D
Stanford Exploration Project
1/13/1998
![\begin{displaymath}
U^{(-)}({\bf r},t)={1 \over \sqrt{\pi d^{(-)}}}{wA_0H[\tau({\bf r})-t] \over
\sqrt{\tau^{(-)}({\bf r})-t}}+\psi({\bf r})\end{displaymath}](img557.gif)
![\begin{displaymath}
U^{(-)}({\bf r},t)={1 \over \sqrt{\pi d^{(-)}}}{wA_0H[\tau({\bf r})-t] \over
\sqrt{\tau^{(-)}({\bf r})-t}}+\psi({\bf r})\end{displaymath}](img557.gif)
![]()
![]()
![]()
![]()
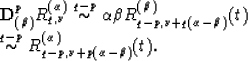
![]()
![]()
![\begin{displaymath}
U^{(-)} \sim {wA_0 \over \sqrt{\vert d^{(-)}\vert}} R^{(+)}_{-{1 \over2}}
[t-\tau^{(-)}({\bf r})]\end{displaymath}](img569.gif)
![\begin{displaymath}
U^{(-)} \sim \kappa {wA_0 \over \sqrt{\vert d^{(-)}\vert}}
R^{(-)}_{-{1 \over2},{1- \kappa \over 2}}
[t-\tau^{(-)}]\end{displaymath}](img570.gif)
![]() and
and ![]() :the order = p if
:the order = p if
![]()
![]()
![]()
![]()
![]()
![]() is a special one if, for given
is a special one if, for given ![]() and
and ![]() ,
,![]() .Each special point of the order p=2 is the point on caustics.
.Each special point of the order p=2 is the point on caustics.