|
|
|
|
Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media |
When the grains in a granular packing are no longer composed of elastically homogeneous and isotropic materials, or if they are homogeneous but anisotropic while nevertheless being distributed in a randomly oriented way in space, then -- as has been pointed out previously in Brown and Korringa (1975), Rice and Cleary (1976), and the work of others [e.g., Wang (2000)] -- I need to introduce a more general notation to deal with these circumstances.
Recall that the Reuss (1929) average of the grain bulk moduli for a heterogeneous medium with a distribution of grain types is given by:
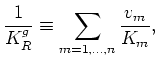 is the volume fraction (out of all the solid material present,
so that
is the volume fraction (out of all the solid material present,
so that
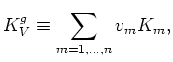 . Furthermore, these two measures are
also known (Hill, 1952; Voigt, 1928; Reuss, 1929) to satisfy
. Furthermore, these two measures are
also known (Hill, 1952; Voigt, 1928; Reuss, 1929) to satisfy
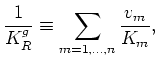 values. However, this fact actually is not pertinent here, as the only averages
of this type that play a direct role in the poroelastic equations are always those of the Reuss-type,
as will be shown in the further developments.
values. However, this fact actually is not pertinent here, as the only averages
of this type that play a direct role in the poroelastic equations are always those of the Reuss-type,
as will be shown in the further developments.
To clarify later usage of the same notation ![]() , I emphasize here that when (or if) the
grains in our assemblage are all anisotropic -- but nevertheless of the same type and oriented
randomly in space -- then the pertinent average is again the Reuss average. But in this case
the average is determined by the equation
, I emphasize here that when (or if) the
grains in our assemblage are all anisotropic -- but nevertheless of the same type and oriented
randomly in space -- then the pertinent average is again the Reuss average. But in this case
the average is determined by the equation
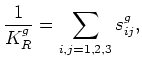 for
for
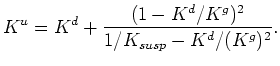 . The formula as quoted in (2)
was only written for the case of homogeneous grains. But if we generalize this formula slightly as:
. The formula as quoted in (2)
was only written for the case of homogeneous grains. But if we generalize this formula slightly as:
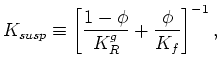 ),
(b) for heterogeneous volumes of isotropic grains [when
),
(b) for heterogeneous volumes of isotropic grains [when If the clumpings are loose enough, then the fluid can act equally on all the individual grains, and the result in (9) holds true regardless of the heterogeneity. However, if this is not the case, then there must be elastically distinct clumpings of grains forming solid composites locally - so the individual grains are no longer uniformly surrounded by the pore fluid. Then, each grain's fluid environment is different, due to welded contacts with other contiguous grains. I am assuming for the present purposes that such effects are negligible in the types of comparatively homogeneous porous media (on the meso- and macroscales, but not necessarily on the microscale) being studied here. In fact, some types of more heterogeneous systems can be treated, and some of these have already been studied (Berryman and Milton, 1991; Berryman and Pride, 2002) when the porous system is composed of just two distinct types of grain clumpings; however, I will not be discussing such double-porosity and/or multi-porosity effects in the present paper.
|
|
|
|
Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media |