|
|
|
|
Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media |
Another important type of heterogeneity that can occur in practice involves heterogeneity of the pore space. One obvious issue is whether the pores are all connected to each other, or whether there may be two (or more) distinct, but intertwining, pore systems. One well-known example of this situation is the double-porosity concept (Barenblatt and Zheltov, 1960; Gurevich et al., 2009; Berryman and Pride, 2002), in which one type of pore has high volume but low permeability, while the other has low volume (imagine a system of very flat cracks or fractures) and high permeability. I can also consider that some pores might be interior to some grains and not connected to any other pores (and might therefore also be empty of pore fluid), while other subsets of the grains have no inherent porosity of this type, and so are truly solid grains.
I will not try to deal with all these cases simultaneously, as even enumerating all the possibilities quickly becomes burdensome. I will limit myself instead to one of the more typical scenarios, considered for example by Brown and Korringa (1975) and by Rice and Cleary (1976) -- and also see the recent related work of Gurevich et al. (2009).
Heterogeneity of the pore space is most important when considering flow of fluid into and out of the boundaries of
a porous sample. Then, the concept of increment of fluid content ![]() comes into play, and special care is
required. A straightforward definition of this dimensionless parameter
(just as the strains
comes into play, and special care is
required. A straightforward definition of this dimensionless parameter
(just as the strains ![]() ,
, ![]() ,
, ![]() ,
, ![]() are all dimensionless) is given by:
are all dimensionless) is given by:
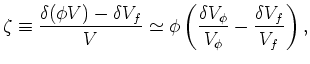 is the overall volume of the initially fully fluid-saturated porous material at the first instant of consideration,
is the overall volume of the initially fully fluid-saturated porous material at the first instant of consideration,
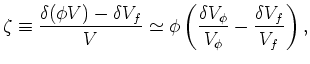 that can either supply more fluid or absorb any excreted fluid as needed during the
nonstationary phase of the poroelastic process; the amount of pore fluid can therefore either increase or decrease
from the initial amount of pore fluid, and at the same time the pore volume can also be changing, but not necessarily at
exactly the same rate as the pore fluid itself. The one exception to these statements is when the surface pores
of the total volume
that can either supply more fluid or absorb any excreted fluid as needed during the
nonstationary phase of the poroelastic process; the amount of pore fluid can therefore either increase or decrease
from the initial amount of pore fluid, and at the same time the pore volume can also be changing, but not necessarily at
exactly the same rate as the pore fluid itself. The one exception to these statements is when the surface pores
of the total volume 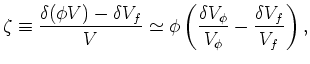 are sealed, in which case the system is ``undrained'' and
are sealed, in which case the system is ``undrained'' and
 and
and
It can also be shown using poroelastic reciprocity (and I will show this later as it very clearly develops in the following anisotropic analysis) that
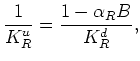 and
and
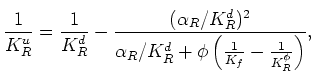 , then
(19) reduces exactly to (1). Although this result is the same
as that of Brown and Korringa (1975), I nevertheless write it differently to emphasize different features.
, then
(19) reduces exactly to (1). Although this result is the same
as that of Brown and Korringa (1975), I nevertheless write it differently to emphasize different features.
|
|
|
|
Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media |