|
|
|
|
Target-oriented least-squares migration/inversion with sparseness constraints |
| (9) |
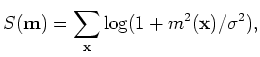 is a scalar parameter of the Cauchy distribution that controls the sparsity of the model.
The objective function 8 can be minimized under
is a scalar parameter of the Cauchy distribution that controls the sparsity of the model.
The objective function 8 can be minimized under | (10) |
| (11) |
|
|
|
|
Target-oriented least-squares migration/inversion with sparseness constraints |