|
|
|
|
Target-oriented least-squares migration/inversion with sparseness constraints |
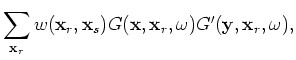 is the angular frequency,
and
is the angular frequency,
and
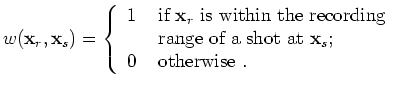 , we obtain the diagonal elements of the Hessian; when
, we obtain the diagonal elements of the Hessian; when
|
|
|
|
Target-oriented least-squares migration/inversion with sparseness constraints |