Target-oriented least-squares migration/inversion with sparseness constraints

Hessian by phase encoding

The truncated Hessian operator can be computed by using equation 5, but direct implementation of equation 5 requires storing a huge number of Green's functions (especially in 3-D), which may bring computational challenges for large-scale applications. An alternative and also more efficient way is to compute the Hessian using the so-called phase-encoding method (Tang, 2008a,b), where equation 5 is structured into a similar form as that of the wave-equation migration, except for a modified boundary condition for the receiver wavefield and a modified imaging condition which correlates four wavefields instead of two. Doing so makes storing Green's functions unnecessary, and the cost for computing a target-orineted wave-equation Hessian becomes comparable to one migration.

As further discussed by Tang (2008a), the phase-encoded Hessian is equivalent to the imaging Hessian in the generalized source and receiver domain, a transformed domian that is obtained by linear combination of the encoded sources and receivers. Different phase-encoded Hessian therefore can be obtained through different encoding strategies: if the encoding is performed in the source domain, we get the source-side encoded Hessian; if the encoding is performed in the receiver domain, we get the receiver-side encoded Hessian; if the encoding is performed in both source and receiver domain, we get the source- and receiver-side simultaneously encoded Hessian. One shortcoming of the encoding method, however, is that it also introduces undesired crosstalk artifacts, which may affect the convergence of the model-space based inversion (Tang, 2008b). The crosstalk artifacts can be effectively suppressed by carefully choosing the phase-encoding functions. As demonstrated by Tang (2008a,b), plane-wave-phase encoding or random-phase encoding or a combination of the two can effectively attenuate the crosstalk.

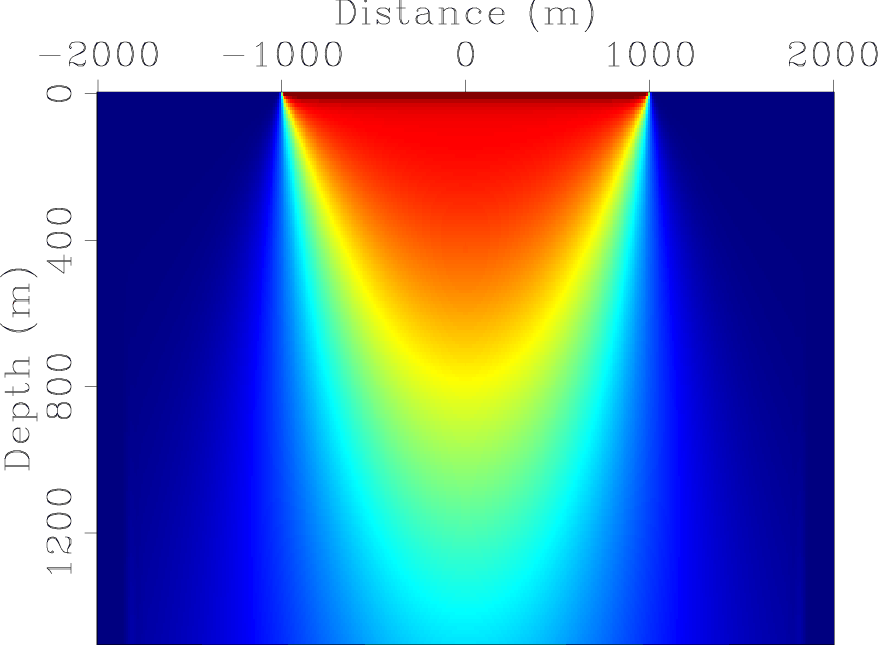
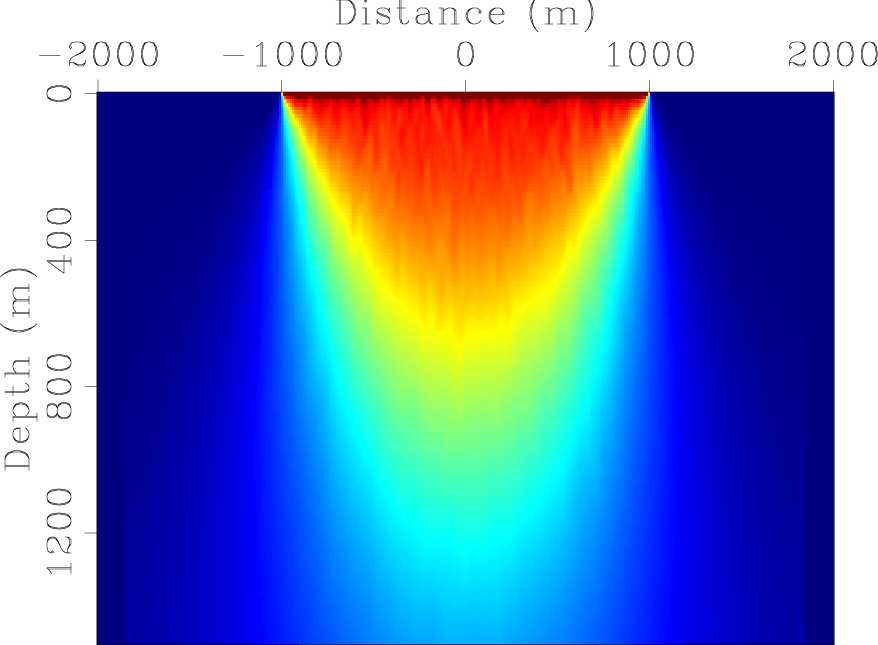
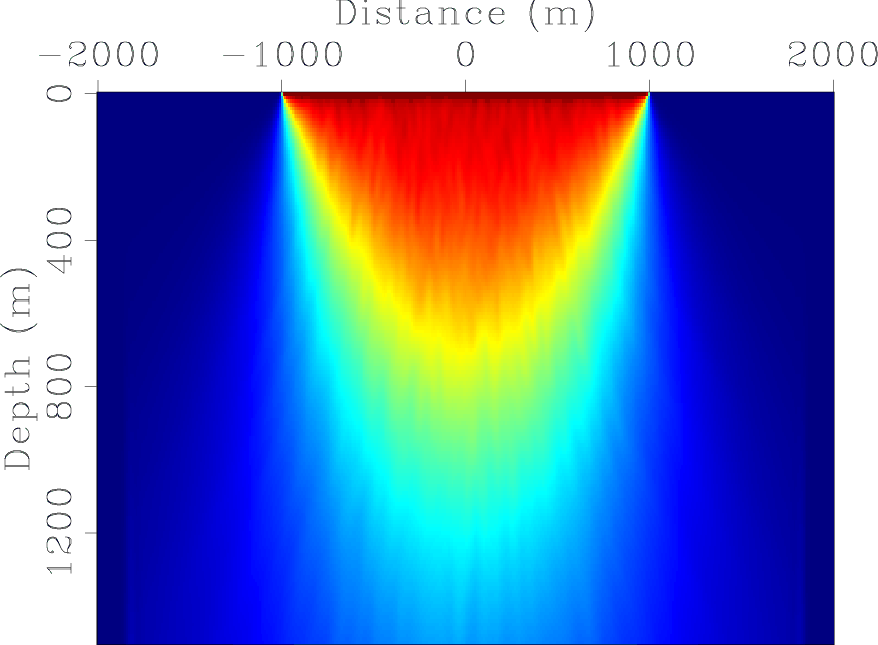
Figure 1 compares diagonal parts of the exact Hessian (Figure 1(a)) obtained using equation 5 and the phase-encoded Hessians (Figure 1(b) for the receiver-side randomly phase-encoded Hessian and Figure 1(c) for the simultaneously phase-encoded Hessian with a mixed encoding strategy) for a simple model with a constant velocity of $2000$ m/s. The acquisition geometry consists of $201$ shots from $-1000$ m to $1000$ m with a $10$ m sampling and $201$ receivers also spanning from $-1000$ m to $1000$ m with a $10$ m sampling. Figure 2 compares the off-diagonal elements (a row of the truncted Hessian matrix) for image point at $x=0$ m, $z=800$ m. The size of the filter is $21\times21$ in $x$ and $z$ directions. The comparisons show that besides lower computational cost, the phase-encoded Hessians are good approximations to the exact truncated Hessian.

hess-exact,hess-random,hess-simul-mixed
Figure 1. The diagonal part of the Hessian for a constant-velocity model. (a) The exact Hessian; (b) the receiver-side randomly phase-encoded Hessian and (c) the simultaneously phase-encoded Hessian with a mixed phase encoding which combines both random and plane-wave encoding functions. [CR]

hess-exact-offd1,hess-random-offd1,hess-simul-mixed-offd1
Figure 2. The off-diagonal elements of the Hessian for a image point (a row of the Hessian). (a) The exact Hessian; (b) the receiver-side randomly phase-encoded Hessian and (c) the simultaneously phase-encoded Hessian with a mixed phase encoding which combines both random and plane-wave encoding functions. [CR]

Target-oriented least-squares migration/inversion with sparseness constraints