




Next: GASSMANN'S EQUATIONS AND FRACTURED
Up: ANISOTROPY DUE TO FRACTURES
Previous: Thomsen parameters
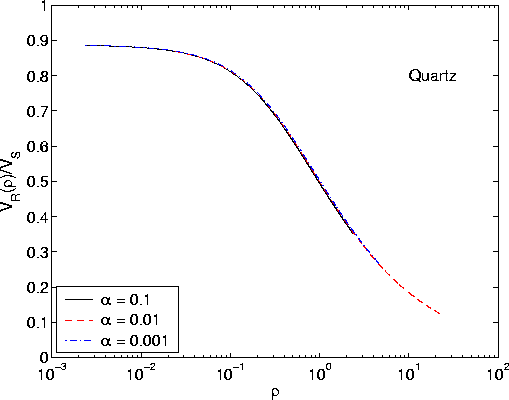
Qrtzsemilogvrvs3b_rho
Figure 3
Computation of Rayleigh wave speed in quartz with
horizontally aligned cracks for three choices of penny-crack
aspect ratio, and a range of values of the crack density 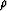 .If the assumption/prediction that aspect ratio is does not really
matter, just crack density, then all three curves should overlap,
as they do here at the lower crack densities. .If the assumption/prediction that aspect ratio is does not really
matter, just crack density, then all three curves should overlap,
as they do here at the lower crack densities.
|
|  |

Now, to provide one simple illustration of the use of what has been
presented so far, consider the well-known formula for the Rayleigh
wave speed v = vR in an isotropic medium [see Ewing et al. (1957),
Al-Husseini et al. (1981), Weertman (1996)]:
| 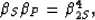 |
(6) |
where  ,
, 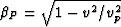 ,
,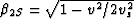 , with vs being the (isotropic)
shear wave speed and vp being the (isotropic) compressional wave
speed in the host medium.
For an anisotropic medium having the same transversely isotropic (VTI)
symmetry that I have been considering (for the case of randomly oriented
vertical cracks), Musgrave (1959) shows that the equivalent
result for the Rayleigh wave speed v = vR in the plane
perpendicular to the VTI axis of symmetry is determined by the cubic equation
, with vs being the (isotropic)
shear wave speed and vp being the (isotropic) compressional wave
speed in the host medium.
For an anisotropic medium having the same transversely isotropic (VTI)
symmetry that I have been considering (for the case of randomly oriented
vertical cracks), Musgrave (1959) shows that the equivalent
result for the Rayleigh wave speed v = vR in the plane
perpendicular to the VTI axis of symmetry is determined by the cubic equation
| 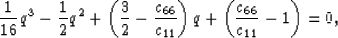 |
(7) |
where 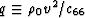 and
and 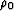 is the density of the
medium (which is assumed to be the same as that of the pure material
without cracks,
since the cracks are very flat and are not introducing any
significant amount of porosity). [It is not difficult to check that
(6) and (7)
are equivalent when the elastic medium is isotropic.]
is the density of the
medium (which is assumed to be the same as that of the pure material
without cracks,
since the cracks are very flat and are not introducing any
significant amount of porosity). [It is not difficult to check that
(6) and (7)
are equivalent when the elastic medium is isotropic.]
From the definitions of 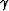 and
and  , it is now
straightforward to see that
, it is now
straightforward to see that
| 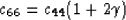 |
(8) |
and
| 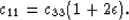 |
(9) |
Shear modulus 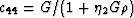 , while
c33 is found by inverting
, while
c33 is found by inverting 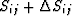 for the 33
component of the stiffness matrix.
So we can now easily compute the Rayleigh wave speed
by solving the cubic equation (7).
Some results of this type are displayed in Figure 3.
In particular, we find that the crack density is indeed
a good parameter to use, as all these plots for different choices of
crack aspect ratio clearly overlap to numerical accuracy
in the low crack density range.
for the 33
component of the stiffness matrix.
So we can now easily compute the Rayleigh wave speed
by solving the cubic equation (7).
Some results of this type are displayed in Figure 3.
In particular, we find that the crack density is indeed
a good parameter to use, as all these plots for different choices of
crack aspect ratio clearly overlap to numerical accuracy
in the low crack density range.





Next: GASSMANN'S EQUATIONS AND FRACTURED
Up: ANISOTROPY DUE TO FRACTURES
Previous: Thomsen parameters
Stanford Exploration Project
4/5/2006


![]() and
and ![]() , it is now
straightforward to see that
, it is now
straightforward to see that