Thomsen parameters

If we have the compliance correction matrix $\Delta S_{ij}$,then we can quickly find expressions for the Thomsen seismic wave parameters for weak anisotropy (Thomsen, 1986; 1995; 2002; Rathore et al., 1995; Rüger, 1998; 2002; Grechka, 2005). Clearly, a weak anisotropy assumption is also consistent with the small crack density assumption that was needed above to justify the use of the Sayers and Kachanov (1991) method.

There are three Thomsen parameters: $\gamma$,$\epsilon$, and $\delta$. Parameter $\gamma$ is essentially the fractional difference between the SH-wave velocities in the horizontal and vertical directions for a VTI medium. Similarly, parameter $\epsilon$ is essentially the difference between the P-wave velocities in the horizontal and vertical directions. Parameter $\delta$ is more difficult to interpret, but contributes in an essential way both to near vertical P-wave speed variations, and also to the angular dependence of the SV-wave speed. There are a great many steps that go into Thomsen parameter calculations since the crack density effects are most conveniently expressed in terms of the compliance matrix while the Thomsen parameters are usually defined instead in terms of the stiffness matrix (inverse of the compliance matrix). I will not show my work here, but merely quote the final result for the case of randomly oriented vertical fractures considered in the previous subsection.

For present purposes, I just want to show in a quick way how this method works, so I will concentrate on the easiest two parameters which are $\gamma$ and $\epsilon$. For these two parameters, I have the following results:  

$$\gamma = \frac{c_{66}-c_{44}}{2c_{44}} = - \eta_2\rho\frac{E}{4(1+\nu)} = -\eta_2\rho\frac{G}{2},$$ (4)

and  

$$\epsilon = \frac{c_{11} - c_{33}}{2c_{33}} = -[(1+\nu)\eta_1... ...]\rho\frac{E}{2(1-\nu^2)} \simeq - \eta_2\rho\frac{G}{1-\nu},$$ (5)

where $\nu = (K-2G/3)/2(K+G/3)$ is Poisson's ratio, E is related to the host medium's bulk (K) and shear (G) moduli by 1/E = 1/9K + 1/3G, and $G = E/2(1+\nu)$. In the second expression of (5), I have neglected the term proportional to $\eta_1\rho$ as this term is normally very small (on the order of $1\%$ of the term retained). It can also be shown that for this model the remaining Thomsen parameter $\delta$ takes exactly the same value as $\epsilon$ to lowest order in the crack density parameter.

 

thomsenALLv Figure 2 Computed values of the Thomsen parameters 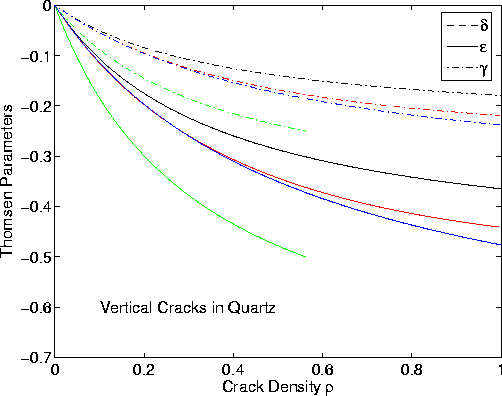$\delta$,$\epsilon$, $\gamma$, for four distinct EMT models: noninteracting (black), CPA (red), DS (blue) and the Budiansky-O'Connell self consistent (green). The parameter $\delta$ is not seen separately here because for this choice of crack microstructure (randomly oriented vertical cracks) $\delta = \epsilon$ to the order to which we are working, for small crack densities.

Examples of Thomsen's parameters for various choices of EMT are displayed in Figure 2. The results illustrate how estimates of $\eta_1$ and $\eta_2$ obtained from four different isotropic estimation schemes [noninteracting, DS (Zimmerman, 1991), CPA (Berryman, 1980), and nonsymmetric self-consistent scheme of Budiansky and O'Connell (1976), and O'Connell and Budiansky (1977)] can then be used to predict what values Thomsen's parameters should take in field data.

Some judgment is required then as to the most appropriate EMT to use, and prior work shows that some knowledge of microstructure can serve as a very useful guide when making this choice (Berge et al., 1993a; 1995).