




Next: DECONSTRUCTION
Up: Berryman: Seismic waves in
Previous: Rayleigh wave speed
It is also important to make a connection between the fracture results quoted
above and Gassmann's results (Gassmann, 1951; Berryman, 1999)
for fluid saturated and undrained porous
media. Even very flat cracks could harbor some fluid at various times
and the question is how this fluid affects the response of the
cracks.
Recall first that Gassmann's result on the effect of fluids in a
porous medium in anisotropic media can be expressed by using
a compliance correction matrix of the form:
| 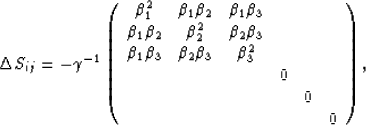 |
(10) |
where the fluid bulk modulus appears only in the factor 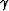 ,and the coefficients
,and the coefficients 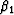 ,
,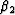 ,
,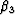 satisfy a sumrule of
the form
satisfy a sumrule of
the form 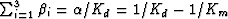 ,and
,and 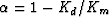 is the Biot-Willis coefficient (Biot and
Willis, 1957). The bulk
moduli Kd and Km are, respectively,
the drained (porous) bulk modulus of the overall
system and the mineral modulus whenever there is only one mineral
present in the system (as I will assume here for the present).
[The scalar drained modulus Kd for an anisotropic system is
identical to the Reuss average for the bulk modulus of the compliance matrix.]
When the system is responding anisotropically as in the case of
a set of cracks having vertical symmetry axis in the example
(3), we can easily make (10)
compatible with the structure of (3) by first ignoring
the coefficient
is the Biot-Willis coefficient (Biot and
Willis, 1957). The bulk
moduli Kd and Km are, respectively,
the drained (porous) bulk modulus of the overall
system and the mineral modulus whenever there is only one mineral
present in the system (as I will assume here for the present).
[The scalar drained modulus Kd for an anisotropic system is
identical to the Reuss average for the bulk modulus of the compliance matrix.]
When the system is responding anisotropically as in the case of
a set of cracks having vertical symmetry axis in the example
(3), we can easily make (10)
compatible with the structure of (3) by first ignoring
the coefficient 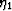 (which is known to be quite small anyway), and
then setting
(which is known to be quite small anyway), and
then setting 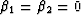 .No other possibiities are available. This means that Gassmann's
results are introduced into the anisotropic problem by making a fluid-dependent
perturbation to
.No other possibiities are available. This means that Gassmann's
results are introduced into the anisotropic problem by making a fluid-dependent
perturbation to 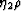 and ignoring
and ignoring 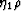 , since its value
is two orders of magnitude smaller.
, since its value
is two orders of magnitude smaller.
Gassmann's formula for an isotropic medium can be written in the form:
| 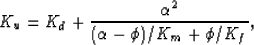 |
(11) |
where Ku is the undrained bulk modulus, Kd is the drained bulk
modulus,
Km is the mineral or solid modulus, Kf is the bulk modulus of
the pore fluid, 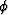 is the porosity and
is the porosity and 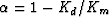 .This result can be rearranged in order to express it in terms of
compliances, instead of stiffnesses, as
.This result can be rearranged in order to express it in terms of
compliances, instead of stiffnesses, as
| ![\begin{displaymath}
\frac{1}{K_u} - \frac{1}{K_d} = -\frac{\alpha}{K_d}\left[1 +...
... \phi}{K_f \alpha}\left(1-\frac{K_f}{K_m}\right)\right]^{-1}.
\end{displaymath}](img49.gif) |
(12) |
Now for fractured media having no other porosity 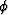 except the
fractures themselves, I have
except the
fractures themselves, I have
| 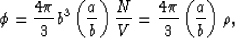 |
(13) |
where the crack density is 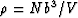 ,N/V is the number of cracks per unit volume,
b is the radius of the (assumed) penny-shaped crack,
and a/b is its aspect ratio.
Substituting (13) into (12) shows that
crack density
,N/V is the number of cracks per unit volume,
b is the radius of the (assumed) penny-shaped crack,
and a/b is its aspect ratio.
Substituting (13) into (12) shows that
crack density 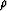 is always multiplied by the factor (1 - Kf/Km)
in Gassmann's formula, and this result thereby provides a convenient
means of introducing the fluid effects into the formulas for
compliance in the presence of distributions of cracks.
is always multiplied by the factor (1 - Kf/Km)
in Gassmann's formula, and this result thereby provides a convenient
means of introducing the fluid effects into the formulas for
compliance in the presence of distributions of cracks.
The preceding review of Gassmann's original derivation shows that it is not
appropriate to replace all occurrences of 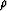 in (1) by
in (1) by
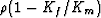 . Only those terms that determine the
strain response to the principle stresses need to be considered.
Furthermore, the analysis of the symmetry conditions has shown
that only those terms involving
. Only those terms that determine the
strain response to the principle stresses need to be considered.
Furthermore, the analysis of the symmetry conditions has shown
that only those terms involving 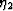 need to be modified.
If we neglect
need to be modified.
If we neglect 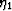 for the remainder of this argument (it is small
anyway -- a 1% effect -- as stated previously),
then we find that, for an isotropic system,
for the remainder of this argument (it is small
anyway -- a 1% effect -- as stated previously),
then we find that, for an isotropic system,
| 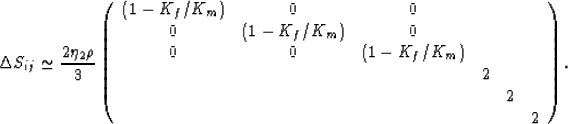 |
(14) |
Changes in the pertinent compliances are therefore given by
| 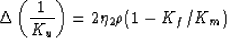 |
(15) |
for the undrained bulk modulus Ku, and
| 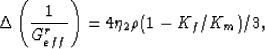 |
(16) |
which is the change in the uniaxial shear modulus due the presence of
cracks containing fluids.
Then, I recover the result of Mavko and Jizba (1991) easily by noting first
that the change in the undrained shear modulus for the isotropic system is
| 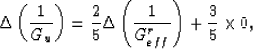 |
(17) |
since there are two equal shear contributions from the upper left hand
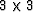 submatrix of (14), while the three remaining
contributions to shear compliance exhibit no fluid dependence and so
do not contribute here. Then, finally, I have
submatrix of (14), while the three remaining
contributions to shear compliance exhibit no fluid dependence and so
do not contribute here. Then, finally, I have
| 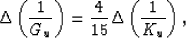 |
(18) |
in agreement with previous results of this type (Berryman et
al., 2002b). So this formalism provides an efficient means of
correctly deriving both old and new results.
Berryman et al. (2002b) show that the factor 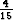 in (18)
holds strictly only for very flat cracks, and that the appropriate
factor in other situations can be either higher or lower than
in (18)
holds strictly only for very flat cracks, and that the appropriate
factor in other situations can be either higher or lower than
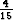 , depending on details. The neglected terms depending
on the Sayers and Kachanov parameter
, depending on details. The neglected terms depending
on the Sayers and Kachanov parameter 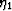 provide very small
corrections to the drained moduli, but actually have no dependence on
fluid saturation, and so have no influence on the relationship between
undrained (fluid saturated) moduli shown in (18).
provide very small
corrections to the drained moduli, but actually have no dependence on
fluid saturation, and so have no influence on the relationship between
undrained (fluid saturated) moduli shown in (18).





Next: DECONSTRUCTION
Up: Berryman: Seismic waves in
Previous: Rayleigh wave speed
Stanford Exploration Project
4/5/2006
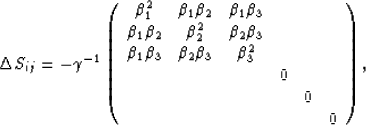
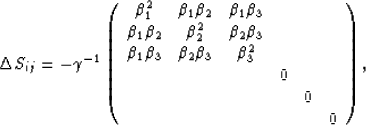
![\begin{displaymath}
\frac{1}{K_u} - \frac{1}{K_d} = -\frac{\alpha}{K_d}\left[1 +...
... \phi}{K_f \alpha}\left(1-\frac{K_f}{K_m}\right)\right]^{-1}.
\end{displaymath}](img49.gif)
![]() in (1) by
in (1) by
![]() . Only those terms that determine the
strain response to the principle stresses need to be considered.
Furthermore, the analysis of the symmetry conditions has shown
that only those terms involving
. Only those terms that determine the
strain response to the principle stresses need to be considered.
Furthermore, the analysis of the symmetry conditions has shown
that only those terms involving ![]() need to be modified.
If we neglect
need to be modified.
If we neglect ![]() for the remainder of this argument (it is small
anyway -- a 1% effect -- as stated previously),
then we find that, for an isotropic system,
for the remainder of this argument (it is small
anyway -- a 1% effect -- as stated previously),
then we find that, for an isotropic system,
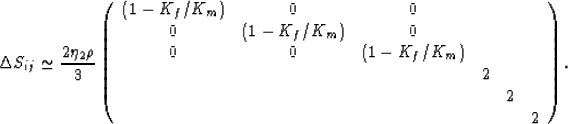
![]() in (18)
holds strictly only for very flat cracks, and that the appropriate
factor in other situations can be either higher or lower than
in (18)
holds strictly only for very flat cracks, and that the appropriate
factor in other situations can be either higher or lower than
![]() , depending on details. The neglected terms depending
on the Sayers and Kachanov parameter
, depending on details. The neglected terms depending
on the Sayers and Kachanov parameter ![]() provide very small
corrections to the drained moduli, but actually have no dependence on
fluid saturation, and so have no influence on the relationship between
undrained (fluid saturated) moduli shown in (18).
provide very small
corrections to the drained moduli, but actually have no dependence on
fluid saturation, and so have no influence on the relationship between
undrained (fluid saturated) moduli shown in (18).